
 如圖,一段拋物線:y=2x(x-3)(0≤x≤3),記為C1,它與x軸交于點O,A1;將C1繞點A1旋轉180°得C2,交x軸于點A2;將C2繞點A2旋轉180°得C3,交x軸于點A3;…,如此進行下去,直至的C10,(1)請寫出拋物線C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段拋物線C10上,則m=-260.
如圖,一段拋物線:y=2x(x-3)(0≤x≤3),記為C1,它與x軸交于點O,A1;將C1繞點A1旋轉180°得C2,交x軸于點A2;將C2繞點A2旋轉180°得C3,交x軸于點A3;…,如此進行下去,直至的C10,(1)請寫出拋物線C2的解析式:y=-2(x-3)(x-6);(2)若P(17,m)在第10段拋物線C10上,則m=-260. 分析 (1)根據圖象的旋轉變化規律以及二次函數的平移規律得出平移后解析式,
(2)利用已知得出圖象與x軸交坐標變化規律,進而求出a的值.
解答 解:(1)∵一段拋物線:y=2x(x-3)(0≤x≤3),記為C1,它與x軸交于點O,A1;將C1繞點A1旋轉180°得C2,
∴C1過(0,0),(3,0)兩點,
∴拋物線C2的解析式二次項系數為:-2,且過點(3,0),(6,0),
∴y=-2(x-3)(x-6);
故答案為:y=-2(x-3)(x-6);
(2)∵一段拋物線:y=2x(x-3)(0≤x≤3),
∴圖象與x軸交點坐標為:(0,0),(3,0),
∵將C1繞點A1旋轉180°得C2,交x軸于點A2;
將C2繞點A2旋轉180°得C3,交x軸于點A3;
…
如此進行下去,直至得C10.
∴C10的與x軸的交點橫坐標為(27,0),(30,0),且圖象在x軸上方,
∴C10的解析式為:y10=-2(x-27)(x-30),
當x=17時,y=-2(17-27)×(17-30)=-260.
故答案為:-260.
點評 此題主要考查了二次函數的平移規律,根據已知得出二次函數旋轉后解析式是解題關鍵.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案科目:初中數學 來源: 題型:選擇題
| A. | k=-2,b=-4 | B. | k=2,b=-4 | C. | k=-4,b=2 | D. | k=4,b=2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=$\frac{1}{2}$(x-1)2-$\frac{1}{2}$ | B. | y=$\frac{1}{2}$(x-$\frac{1}{4}$)2+$\frac{1}{32}$ | C. | y=$\frac{1}{2}$(x-1)2+$\frac{1}{2}$ | D. | y=$\frac{1}{2}$(x-$\frac{1}{4}$)2-$\frac{1}{32}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
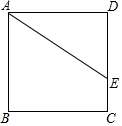 已知正方形ABCD中,點E在邊DC上,DE=3,EC=1,如圖所示,把線段AE繞點A旋轉,使點E落在直線BC上的點F處,則F、C兩點的距離為1或7.
已知正方形ABCD中,點E在邊DC上,DE=3,EC=1,如圖所示,把線段AE繞點A旋轉,使點E落在直線BC上的點F處,則F、C兩點的距離為1或7.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
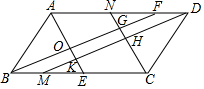 如圖,在平行四邊形ABCD中,AE,BF,CN,DM分別是∠DAB,∠ABC,∠BCD,∠CDA的角平分線,且相交于點O,K,H,G,求證:四邊形HGOK是矩形.
如圖,在平行四邊形ABCD中,AE,BF,CN,DM分別是∠DAB,∠ABC,∠BCD,∠CDA的角平分線,且相交于點O,K,H,G,求證:四邊形HGOK是矩形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com