
分析 根據黃金分割點的定義,知AC為較長線段;則AC=$\frac{\sqrt{5}-1}{2}$AB,代入數據即可得出AC的值,然后計算AB-AC即可得到BC.
解答 解:∵C為線段AB的黃金分割點(AC>BC),
∴AC=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$×10=5$\sqrt{5}$-5,
∴BC=AB-AC=10-(5$\sqrt{5}$-5)=15-5$\sqrt{5}$.
故答案為:15-5$\sqrt{5}$
點評 本題考查了黃金分割:把線段AB分成兩條線段AC和BC(AC>BC),且使AC是AB和BC的比例中項(即AB:AC=AC:BC),叫做把線段AB黃金分割,點C叫做線段AB的黃金分割點.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且線段AB的黃金分割點有兩個.


 怎樣學好牛津英語系列答案
怎樣學好牛津英語系列答案科目:初中數學 來源: 題型:選擇題
| A. | 0和x都是單項式 | B. | -$\frac{2x+y}{2}$與$\frac{1}{x}$都不是單項式 | ||
| C. | a2-3ab+2b3 是三次三項式 | D. | -2πx2y的系數是-2,次數是3 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
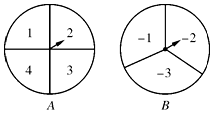 如圖,甲、乙兩人在玩轉盤游戲時,準備了兩個可以自由轉動的轉盤A,B,每個轉盤被分成面積相等的幾個扇形,并在每一個扇形內標上數字.游戲規則:同時轉動兩個轉盤,當轉盤停止后,指針所指區域的數字之和為0時,甲獲勝;數字之和為1時,乙獲勝.如果指針恰好指在分割線上,那么重轉一次,直到指針指向某一區域為止.
如圖,甲、乙兩人在玩轉盤游戲時,準備了兩個可以自由轉動的轉盤A,B,每個轉盤被分成面積相等的幾個扇形,并在每一個扇形內標上數字.游戲規則:同時轉動兩個轉盤,當轉盤停止后,指針所指區域的數字之和為0時,甲獲勝;數字之和為1時,乙獲勝.如果指針恰好指在分割線上,那么重轉一次,直到指針指向某一區域為止.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 正方形ABCD在數軸上的位置如圖所示,點D、A對應的數分別為0和1,若正方形ABCD繞著頂點順時針方向在數軸上連續翻轉,翻轉1次后,點B所對應的數為2;則翻轉2016次后,數軸上數2016所對應的點是( )
正方形ABCD在數軸上的位置如圖所示,點D、A對應的數分別為0和1,若正方形ABCD繞著頂點順時針方向在數軸上連續翻轉,翻轉1次后,點B所對應的數為2;則翻轉2016次后,數軸上數2016所對應的點是( )| A. | 點C | B. | 點D | C. | 點A | D. | 點B |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
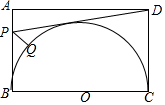 如圖,矩形ABCD中,AB=3,BC=4,P是邊AB上一點,Q是以BC為直徑的圓上一點,則DP+PQ的最小值為( )
如圖,矩形ABCD中,AB=3,BC=4,P是邊AB上一點,Q是以BC為直徑的圓上一點,則DP+PQ的最小值為( )| A. | 5 | B. | $\sqrt{13}$+2 | C. | $\frac{\sqrt{73}}{2}$+$\frac{1}{2}$ | D. | 3$\sqrt{5}$-2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在平面直角坐標系中,一次函數y=-$\frac{3}{4}$x+12與兩坐標軸分別交于A,B兩點,OM⊥AB,垂足為點M.
如圖,在平面直角坐標系中,一次函數y=-$\frac{3}{4}$x+12與兩坐標軸分別交于A,B兩點,OM⊥AB,垂足為點M.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,連PD,下列結論:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正確的結論是( )
如圖,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC,CE⊥AD交AB于E,BE=CF,BF交CE于P,連PD,下列結論:①AC=AE,②CD=BE,③PB=PF,④DP=BF,其中正確的結論是( )| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ①③ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在⊙O中,OA、OB是半徑,OA⊥OB,C、D是$\widehat{AB}$的三等分點,OC、OD分別交AB于點E、F,求證:AE=CD=BF.
如圖,在⊙O中,OA、OB是半徑,OA⊥OB,C、D是$\widehat{AB}$的三等分點,OC、OD分別交AB于點E、F,求證:AE=CD=BF.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
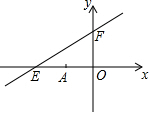 在平面直角坐標系中,一次函數的圖象與坐標軸圍成的三角形,叫做此一次函數的坐標三角形.如圖中的一次函數圖象與x軸、y軸分別相交于點E,F,則△OEF為此函數的坐標三角形.
在平面直角坐標系中,一次函數的圖象與坐標軸圍成的三角形,叫做此一次函數的坐標三角形.如圖中的一次函數圖象與x軸、y軸分別相交于點E,F,則△OEF為此函數的坐標三角形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com