
 已知如圖,正方形ABCD的邊長為2,點E為邊AD上任意一點,連BE,以BE為邊作正方形BEMN,EM、CD相交于點F,過M作MH⊥CD于H,①若∠ABE=30°,則DE=1;②DF的最大值為$\frac{1}{2}$;③MH=AE;④若H為CF的中點,則tan∠CBN=$\frac{\sqrt{5}-1}{2}$,上述說法正確的個數是( )
已知如圖,正方形ABCD的邊長為2,點E為邊AD上任意一點,連BE,以BE為邊作正方形BEMN,EM、CD相交于點F,過M作MH⊥CD于H,①若∠ABE=30°,則DE=1;②DF的最大值為$\frac{1}{2}$;③MH=AE;④若H為CF的中點,則tan∠CBN=$\frac{\sqrt{5}-1}{2}$,上述說法正確的個數是( )| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 ①先根據30°的正切求AE的長,所以由正方形的邊長可以求出DE≠1;
②設AE=x,則DE=2-x,根據同角的三角函數列式為:$\frac{AE}{AB}=\frac{DF}{ED}$,得關于x的方程,解出即得DF的二次函數關系式,求最值即可;
③如圖1,作輔助線,先證明N和G重合,再證明△BAE≌△NHM可得結論;
④設CN=x,HC=y,根據△NHM∽△MHF,列比例式可求得:x=$\frac{1±\sqrt{5}}{2}$y,在直角△BCN中根據正切的定義代入求值.
解答 解:①∵四邊形ABCD為正方形,
∴∠A=90°,
在Rt△ABE中,tan30°=$\frac{AE}{AB}$,
∴AE=$\frac{\sqrt{3}}{3}$×2=$\frac{2\sqrt{3}}{3}$,
∴DE=AD-AE=2-$\frac{2\sqrt{3}}{3}$≠1,
所以此選項不正確;
②設AE=x,則DE=2-x,
∵∠BEM=90°,
∴∠AEB+∠MED=90°,
∵∠AEB+∠ABE=90°,
∴∠MED=∠ABE,
∴tan∠ABE=tan∠MED,
∴$\frac{AE}{AB}=\frac{DF}{ED}$,
∴$\frac{x}{2}=\frac{DF}{2-x}$,
∴DF=-$\frac{1}{2}{x}^{2}$+x,
∵-$\frac{1}{2}$<0,
∴DF有最大值,
則DF的最大值是:$\frac{4×(-\frac{1}{2})×0-{1}^{2}}{4×(-\frac{1}{2})}$=$\frac{1}{2}$,
所以此選項正確;
③如圖1,延長DC,交直線BN于G,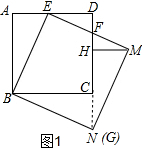
∵四邊形ABCD為正方形,
∴AB=BC,∠A=∠BCG=90°,
∵∠ABE+∠EBC=90°,∠EBC+∠GBC=90°,
∴∠ABE=∠GBC,
∴△ABE≌△CBG,
∴BE=BG,
∵四邊形EBNM是正方形,
∴BE=BN=NM,
∴N和G重合,
∵∠EMN=∠BEM=90°,
∴∠EMH+∠HMN=90°,∠BEA+∠DEM=90°,
∵AD∥HM,
∴∠DEM=∠EMH,
∴∠HMN=∠BEA,
∵∠A=∠NHM=90°,
∴△BAE≌△NHM,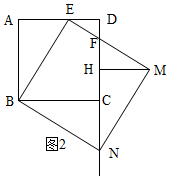
∴AE=MH,
所以此選項正確;
④若H為CF的中點,如圖2,
CH=FH,
設CN=x,HC=y,則HM=x,FH=y,BC=HN=x+y,
∵∠FMN=∠NHM=90°,
∴∠HNM+∠NFM=90°,∠HNM+∠NMH=90°,
∴∠NFM=∠NMH,
∵∠NHM=∠FHM=90°,
∴△NHM∽△MHF,
∴$\frac{NH}{MH}=\frac{HM}{HF}$,
∴MH2=NH•HF,
∴x2=y(x+y),
x=$\frac{1±\sqrt{5}}{2}$y,
∵x>0,
∴x=$\frac{1+\sqrt{5}}{2}$y,
∴BC=x+y=$\frac{3+\sqrt{5}}{2}$y,
∴tan∠CBN=$\frac{CN}{BC}$=$\frac{\frac{1+\sqrt{5}}{2}y}{\frac{3+\sqrt{5}}{2}y}$=$\frac{\sqrt{5}-1}{2}$,
所以此選項正確;
上述說法正確的是②③④,有3個;
故選C.
點評 本題是四邊形的綜合題,考查了正方形的性質、三角形全等、相似的性質和判定、三角函數以及二次函數的最值問題,在正方形中常利用同角的余角相等證明兩個角相等,為全等或相似創造條件.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題
 如圖是校園花圃一角,有的同學為了省時間圖方便,在花圃中踩出了一條小道,這些同學這樣做的數學道理是( )
如圖是校園花圃一角,有的同學為了省時間圖方便,在花圃中踩出了一條小道,這些同學這樣做的數學道理是( )| A. | 點動成線 | B. | 兩點之間直線最短 | ||
| C. | 兩點之間線段最短 | D. | 兩點確定一條直線 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2,5 | B. | 2,2 | C. | 5,7 | D. | 2,7 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
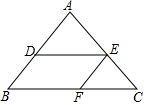 如圖,在△ABC中,DE∥BC,EF∥AB,下列各式中:①$\frac{AD}{DB}$=$\frac{AE}{AC}$;②$\frac{CE}{AC}$=$\frac{CF}{BC}$;③$\frac{EF}{AB}$=$\frac{CE}{CF}$;④$\frac{AD}{AB}$=$\frac{DE}{BC}$;⑤$\frac{AE}{EC}$=$\frac{FC}{BF}$,正確的是②④.
如圖,在△ABC中,DE∥BC,EF∥AB,下列各式中:①$\frac{AD}{DB}$=$\frac{AE}{AC}$;②$\frac{CE}{AC}$=$\frac{CF}{BC}$;③$\frac{EF}{AB}$=$\frac{CE}{CF}$;④$\frac{AD}{AB}$=$\frac{DE}{BC}$;⑤$\frac{AE}{EC}$=$\frac{FC}{BF}$,正確的是②④.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3.2+x=6 | B. | 3.2x=6 | C. | 3.2(1+x)=6 | D. | 3.2(1+x)2=6 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com