
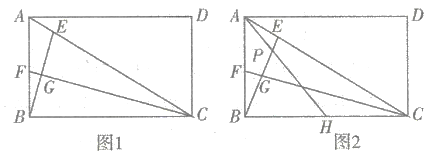
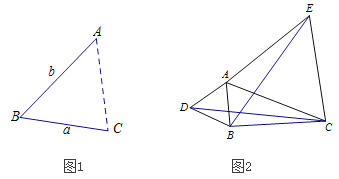
【題目】如圖,在矩形![]() 中,點
中,點![]() 是對角線
是對角線![]() 上一動點,連接
上一動點,連接![]() ,作
,作![]() 分別交
分別交![]() 于點
于點![]() ,
,![]() 于點
于點 ![]() .
.
(1)如圖1,若![]() 恰好平分
恰好平分![]() ,求證:
,求證:![]() ;
;
(2)如圖2,若![]() ,取
,取![]() 的中點
的中點![]() ,連接
,連接![]() 交
交![]() 于點
于點 ![]() .
.
求證:①![]() ;②
;②![]() .
.
【答案】(1)見解析;(2)①見解析;②見解析
【解析】
(1)利用∠ECG=∠BCG,∠CGE=∠CGB,CG=CG即可得證;
(2)①過H作HM∥BE交AC于點M,則CM:ME=CH:HB,由點H為BC的中點,可轉化得到EM=CM,再利用HM∥BE及![]() 即可證得
即可證得![]() ;
;
②延長BE交AD于點N,由△APN∽△HPB可得![]() ,通過證明△ABN∽△BCF可得
,通過證明△ABN∽△BCF可得![]() 進而可轉化為
進而可轉化為![]() .
.
證明:(1)∵CF平分∠BCA
∴∠ECG=∠BCG,
∵CF⊥BE,
∴∠CGE=∠CGB=90°,
在Rt△CGE和Rt△CGB中,
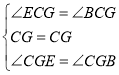 ,
,
∴△CGE≌△CGB(ASA);
(2)①如圖,過H作HM∥BE交AC于點M,

則CM:ME=CH:HB,
∵點H為BC的中點,
∴CH=BH,
∴EM=CM,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵HM∥BE,
∴![]() ,
,
∴![]() ;
;
②如圖,延長BE交AD于點N,
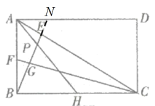
∵在矩形ABCD中,AD∥BC,
∴△APN∽△HPB,
∴![]() ,
,
∴![]() ,
,
∵CF⊥BE,
∴![]() ,
,
∵![]() ,
,
∴∠BCF=∠ABN,
∵∠FBC=∠NAB,
∴△ABN∽△BCF,
∴![]() ,
,
∴![]() ,
,
∵點H為BC的中點,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
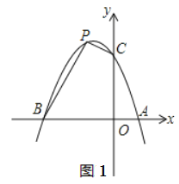
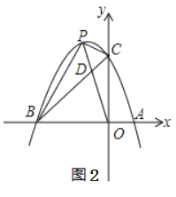
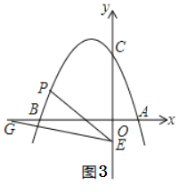
【題目】已知拋物線y=ax2+bx+3經過點A (1,0)和點B (-3,0),與y軸交于點C,點P為第二象限內拋物線上的動點.
(1)拋物線的解析式為__________,拋物線的項點坐標為__________;
(2)如圖1,是否存在點P,使四邊形BOCP的面積為8?若存在,請求出點P的坐標;若不存在,請說明理由.
(3)如圖2,連接OP交BC于點D,當S△CPD∶S△BPD=1∶2時,請求出點D的坐標;
(4)如圖3,點E的坐標為(0,-1),點G為x軸負半軸上的一點,∠OGE=15°,連接PE,若∠PEG=2∠OGE,請求出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
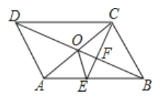
【題目】如圖,已知![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 邊的中點,將
邊的中點,將![]() 繞
繞![]() 點旋轉
點旋轉![]() 得到
得到![]() ,
,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]() .下列結論:①
.下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確的結論有______(只填寫序號).
.其中正確的結論有______(只填寫序號).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】近年來,共享單車逐漸成為高校學生喜愛的“綠色出行”方式之一,許多高校均投放了使用手機支付就可隨取隨用的共享單車.某高校為了解本校學生出行使用共享單車的情況,隨機調查了某天部分出行學生使用共享單車的情況,并整理成如下統計表.
使用次數(次) | 0 | 1 | 2 | 3 | 4 | 5 |
人數(人) | 11 | 15 | 23 | 28 | 20 | 3 |
(1)這天部分出行學生使用共享單車次數的眾數是_________(次).
(2)求這天部分出行學生平均每人使用共享單車的次數.
(3)若該校某天有1500名學生出行,請你估計這天使用共享單車次數在3次以上(含3次)的學生有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校七年級共有500名學生,為了解該年級學生的課外閱讀情況,將從中隨機抽取的40名學生一個學期的閱讀量(閱讀書籍的本數)作為樣本,根據數據繪制了如下的表格和統計圖:
等級 | 閱讀量( | 頻數 | 頻率 |
E | x≤2 | 4 | 0.1 |
D | 2<x≤4 | 12 | 0.3 |
C | 4<x≤6 | a | 0.35 |
B | 6<x≤8 | c | b |
A | x>8 | 4 | 0.1 |

根據上面提供的信息,回答下列問題:
(1)統計表中的![]() ,
,![]() ;并補全條形統計圖;
;并補全條形統計圖;
(2)根據抽樣調查結果,請估計該校七年級學生一學期的閱讀量為“![]() 等”的有多少人?
等”的有多少人?
(3)樣本中閱讀量為“![]() 等”的4名學生中有2名男生和2名女生,現從中隨機挑選2名同學參加區里舉行的“語文學科素養展示”活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
等”的4名學生中有2名男生和2名女生,現從中隨機挑選2名同學參加區里舉行的“語文學科素養展示”活動,請用樹狀圖法或列表法求出恰好選中“1男1女”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解初中學生每天在校體育活動的時間(單位:h),隨機調査了該校的部分初中學生.根據調查結果,繪制出如下的統計圖1和圖2.請根據相關信息,解答下列問題:
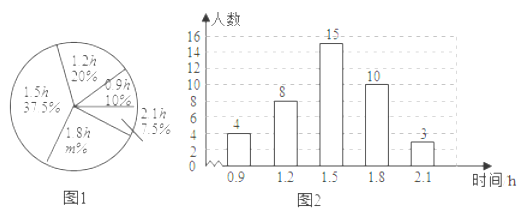
(Ⅰ)本次接受調查的初中學生人數為 ,圖1中m的值為 ;
(Ⅱ)求統計的這組每天在校體育活動時間數據的眾數和中位數;
(Ⅲ)根據統計的這組每天在校體育活動時間的樣本數據,若該校共有1200名初中學生,估計該校每天在校體育活動時間大于1h的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】端午節吃粽子是我國的傳統習俗,某食品廠為了解某市民對去年銷量較好的肉餡粽、豆沙餡粽、紅棗餡粽、蛋黃餡粽(以下分別用A,B,C,D表示)這四種不同口味粽子喜愛情況,在節前對某居民區市民進行了抽樣調查,并將調查情況繪制成下面的兩幅統計圖甲、乙(尚不完整),請根據圖中信息回答:
(1)本次參加抽樣調查的居民有多少人?
(2)若有外形完全相同的A,B,C,D粽各一個,煮熟后,小王吃了兩個,用列表或畫樹狀圖的方法,求他第二個吃到的恰好是C粽的概率.
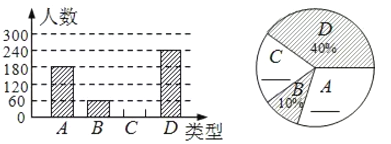
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,點A為線段BC外一動點,且BC=a,AB=b,填空:當點A位于 時,線段AC的長取到最大值,則最大值為 ;(用含a、b的式子表示)。
(2)如圖2,若點A為線段BC外一動點,且BC=4,AB=2,分別以AB,AC為邊,作等邊![]() 和等邊
和等邊![]() ,連接CD,BE.
,連接CD,BE.
①圖中與線段BE相等的線段是線段 ,并說明理由;
②直接寫出線段BE長的最大值為 。
(3)如圖3,在平面直角坐標系中,點A的坐標為(2,0),點B的坐標為(5,0),點P為線段AB外一動點,且PA=2,PM=PB,∠BPM=90°,請直接寫出線段AM長的最大值為 ,及此時點P的坐標為 。(提示:等腰直角三角形的三邊長a、b、c滿足a:b:c=1:1:![]() )
)
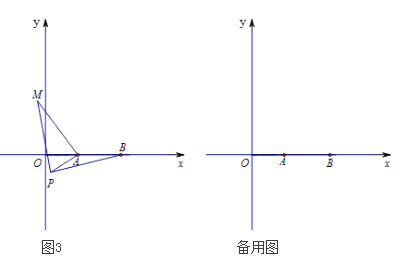
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com