
【題目】在矩形ABCD中,點(diǎn)A關(guān)于∠B的平分線(xiàn)的對(duì)稱(chēng)點(diǎn)為E,點(diǎn)E關(guān)于∠C的平分線(xiàn)的對(duì)稱(chēng)點(diǎn)為F.若AD=![]() AB=2
AB=2![]() ,則AF2=_____.
,則AF2=_____.
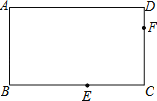
【答案】40﹣16![]()
【解析】
由AD=![]() AB=2
AB=2![]() ,可求得AB=2,AD=2
,可求得AB=2,AD=2![]() ,又由在矩形ABCD中,點(diǎn)A關(guān)于角B的角平分線(xiàn)的對(duì)稱(chēng)點(diǎn)為E,點(diǎn)E關(guān)于角C的角平分線(xiàn)的對(duì)稱(chēng)點(diǎn)為F,根據(jù)軸對(duì)稱(chēng)的性質(zhì),可求得BE,CF的長(zhǎng),繼而求得DF的長(zhǎng),然后由勾股定理求得答案.
,又由在矩形ABCD中,點(diǎn)A關(guān)于角B的角平分線(xiàn)的對(duì)稱(chēng)點(diǎn)為E,點(diǎn)E關(guān)于角C的角平分線(xiàn)的對(duì)稱(chēng)點(diǎn)為F,根據(jù)軸對(duì)稱(chēng)的性質(zhì),可求得BE,CF的長(zhǎng),繼而求得DF的長(zhǎng),然后由勾股定理求得答案.
∵AD=![]() AB=2
AB=2![]() ,
,
∴AB=2,AD=2![]() ,
,
∵四邊形ABCD是矩形,
∴BC=AD=2![]() ,CD=AB=2,
,CD=AB=2,
∵在矩形ABCD中,點(diǎn)A關(guān)于角B的角平分線(xiàn)的對(duì)稱(chēng)點(diǎn)為E,點(diǎn)E關(guān)于角C的角平分線(xiàn)的對(duì)稱(chēng)點(diǎn)為F,
∴BE=AB=2,
∴CF=CE=BC﹣BE=2![]() ﹣2,
﹣2,
∴DF=CD﹣CF=4﹣2![]() ,
,
∴AF2=AD2+DF2=(2![]() )2+(4﹣2
)2+(4﹣2![]() )2=40﹣16
)2=40﹣16![]() .
.
故答案為:40﹣16![]() ;
;



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某市在藝術(shù)節(jié)中組織中小學(xué)校文藝匯演,甲、乙兩所學(xué)校共92名學(xué)生![]() 其中甲校學(xué)生多于乙校學(xué)生,且甲校學(xué)生不足90名
其中甲校學(xué)生多于乙校學(xué)生,且甲校學(xué)生不足90名![]() ,現(xiàn)準(zhǔn)備統(tǒng)一購(gòu)買(mǎi)服裝參加演出,下表是某服裝廠給出的演出服裝價(jià)格表:
,現(xiàn)準(zhǔn)備統(tǒng)一購(gòu)買(mǎi)服裝參加演出,下表是某服裝廠給出的演出服裝價(jià)格表:
購(gòu)買(mǎi)服裝的套數(shù) | 1套至45套 | 46套至90套 | 91套及以上 |
每套服裝的價(jià)格 | 60元 | 50元 | 40元 |
如果兩所學(xué)校單獨(dú)購(gòu)買(mǎi)服裝,一共應(yīng)付5000元
(1)甲、乙兩校各有多少名學(xué)生準(zhǔn)備參加匯演?
(2)如果甲、乙兩校聯(lián)合起來(lái)購(gòu)買(mǎi)服裝,那么比各自購(gòu)買(mǎi)服裝共可以節(jié)省多少錢(qián)?
(3)如果甲校有10名學(xué)生被調(diào)去參加書(shū)法繪畫(huà)比賽不能參加演出,請(qǐng)你為兩校設(shè)計(jì)購(gòu)買(mǎi)服裝方案,并說(shuō)明哪一種最省錢(qián).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】怡然美食店的A、B兩種菜品,每份成本均為14元,售價(jià)分別為20元、18元,這兩種菜品每天的營(yíng)業(yè)額共為1120元,總利潤(rùn)為280元.
(1)該店每天賣(mài)出這兩種菜品共多少份?
(2)該店為了增加利潤(rùn),準(zhǔn)備降低A種菜品的售價(jià),同時(shí)提高B種菜品的售價(jià),售賣(mài)時(shí)發(fā)現(xiàn),A種菜品售價(jià)每降0.5元可多賣(mài)1份;B種菜品售價(jià)每提高0.5元就少賣(mài)1份,如果這兩種菜品每天銷(xiāo)售總份數(shù)不變,那么這兩種菜品一天的總利潤(rùn)最多是多少?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在菱形ABCD中,∠ABC=120°,將菱形折疊,使點(diǎn)A恰好落在對(duì)角線(xiàn)BD上的點(diǎn)G處(不與B、D重合),折痕為EF,若BC=4,BG=3,則GE的長(zhǎng)為________.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】甲、乙兩家超市以相同的價(jià)格出售同樣的商品,為了吸引顧客,各自推出不同的優(yōu)惠方案;在甲超市累計(jì)購(gòu)買(mǎi)商品超出200元之后,超出部分按原價(jià)8折優(yōu)惠;在乙超市累計(jì)購(gòu)買(mǎi)商品超出100元之后,超出部分按原價(jià)8.5折優(yōu)惠,設(shè)顧客購(gòu)物的原費(fèi)用是x元(x>200).
(1)請(qǐng)用含x的代數(shù)式分別表示顧客在兩家超市購(gòu)物所付的實(shí)際費(fèi)用;
(2)李明慧準(zhǔn)備購(gòu)買(mǎi)300元的商品,你認(rèn)為他應(yīng)該去哪家超市?請(qǐng)說(shuō)明理由;
(3)計(jì)算一下,李明慧購(gòu)買(mǎi)多少元的商品時(shí),到兩家超市購(gòu)物所付的費(fèi)用一樣?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
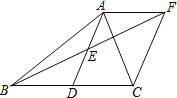
【題目】如圖,已知在△ABC中,D為BC的中點(diǎn),連接AD,E為AD的中點(diǎn),過(guò)點(diǎn)A作BC的平行線(xiàn)交BE的延長(zhǎng)線(xiàn)于點(diǎn)F,連接CF.
(1)求證:四邊形ADCF為平行四邊形.
(2)當(dāng)四邊形ADCF為矩形時(shí),AB與AC應(yīng)滿(mǎn)足怎樣的數(shù)量關(guān)系?請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】閱讀材料并解決問(wèn)題:
(1)數(shù)學(xué)課上,老師提出如下問(wèn)題:
觀察下列算式:
![]() ;
;
![]() ;
;
![]()
![]()
![]()
…
若字母![]() 表示自然數(shù),用含
表示自然數(shù),用含![]() 的式子表示觀察得到的規(guī)律是
的式子表示觀察得到的規(guī)律是![]() ;
;
(2)小云同學(xué)解決完老師提出的問(wèn)題后,又繼續(xù)研究,發(fā)現(xiàn):
①當(dāng)![]() 表示負(fù)整數(shù)且
表示負(fù)整數(shù)且![]() 時(shí),上述規(guī)律仍舊成立;
時(shí),上述規(guī)律仍舊成立;
②當(dāng)![]() 表示分?jǐn)?shù)且
表示分?jǐn)?shù)且![]() 時(shí),上述規(guī)律仍舊成立.
時(shí),上述規(guī)律仍舊成立.
請(qǐng)你對(duì)小云的兩個(gè)發(fā)現(xiàn)進(jìn)行驗(yàn)證,每個(gè)發(fā)現(xiàn)舉出一個(gè)算式;
(3)請(qǐng)你參照小云同學(xué)的研究思路,進(jìn)行猜想,驗(yàn)證、歸納,當(dāng)![]() 時(shí),
時(shí),![]() (用含
(用含![]() 的代數(shù)式表示);
的代數(shù)式表示);
(4)進(jìn)一步進(jìn)行猜想、驗(yàn)證、歸納,當(dāng)![]() (
(![]() 為有理數(shù))時(shí),
為有理數(shù))時(shí),![]() (用含
(用含![]() ,
,![]() ,
,![]() 的代數(shù)式表示)。
的代數(shù)式表示)。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某廠按用戶(hù)的月需求量![]() (件)完成一種產(chǎn)品的生產(chǎn),其中
(件)完成一種產(chǎn)品的生產(chǎn),其中![]() .每件的售價(jià)為18萬(wàn)元,每件的成本
.每件的售價(jià)為18萬(wàn)元,每件的成本![]() (萬(wàn)元)是基礎(chǔ)價(jià)與浮動(dòng)價(jià)的和,其中基礎(chǔ)價(jià)保持不變,浮動(dòng)價(jià)與月需求量
(萬(wàn)元)是基礎(chǔ)價(jià)與浮動(dòng)價(jià)的和,其中基礎(chǔ)價(jià)保持不變,浮動(dòng)價(jià)與月需求量![]() (件)成反比.經(jīng)市場(chǎng)調(diào)研發(fā)現(xiàn),月需求量
(件)成反比.經(jīng)市場(chǎng)調(diào)研發(fā)現(xiàn),月需求量![]() 與月份
與月份![]() (
(![]() 為整數(shù),
為整數(shù),![]() )符合關(guān)系式
)符合關(guān)系式![]() (
(![]() 為常數(shù)),且得到了表中的數(shù)據(jù).
為常數(shù)),且得到了表中的數(shù)據(jù).
月份 | 1 | 2 |
成本 | 11 | 12 |
需求量 | 120 | 100 |
(1)求![]() 與
與![]() 滿(mǎn)足的關(guān)系式,請(qǐng)說(shuō)明一件產(chǎn)品的利潤(rùn)能否是12萬(wàn)元;
滿(mǎn)足的關(guān)系式,請(qǐng)說(shuō)明一件產(chǎn)品的利潤(rùn)能否是12萬(wàn)元;
(2)求![]() ,并推斷是否存在某個(gè)月既無(wú)盈利也不虧損;
,并推斷是否存在某個(gè)月既無(wú)盈利也不虧損;
(3)在這一年12個(gè)月中,若第![]() 個(gè)月和第
個(gè)月和第![]() 個(gè)月的利潤(rùn)相差最大,求
個(gè)月的利潤(rùn)相差最大,求![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
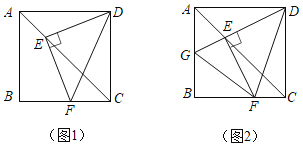
【題目】如圖1,在正方形ABCD中,點(diǎn)E,F分別是AC,BC上的點(diǎn),且滿(mǎn)足DE⊥EF,垂足為點(diǎn)E,連接DF.
(1)求∠EDF= (填度數(shù));
(2)延長(zhǎng)DE交AB于點(diǎn)G,連接FG,如圖2,猜想AG,GF,FC三者的數(shù)量關(guān)系,并給出證明;
(3)①若AB=6,G是AB的中點(diǎn),求△BFG的面積;
②設(shè)AG=a,CF=b,△BFG的面積記為S,試確定S與a,b的關(guān)系,并說(shuō)明理由.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com