
某大學校園內一商店,銷售一種進價為每件20元的臺燈.銷售過程中發現,每月銷售量y(件)與銷售單價x(元)之間的關系可近似的看作一次函數: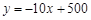 .
.
(1)設此商店每月獲得利潤為w(元),求w與x的函數關系式,并求出w的最大值;
(2)如果此商店想要每月獲得2000元的利潤,那么銷售單價應定為多少元?
(3)根據物價部門規定,這種臺燈的銷售單價不得高于32元,如果此商店想要每月獲得的利潤不低于2000元,那么商店每月的成本最少需要多少元?
(1)w=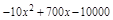 ,2250;(2)30元或40元;(3)3600元
,2250;(2)30元或40元;(3)3600元
【解析】
試題分析:(1)根據總利潤=單利潤×數量,即可得到w與x的函數關系式,再根據二次函數的性質即可得到結果;
(2)根據每月獲得2000元的利潤結合(1)中的函數關系式即可列方程求解;
(3)由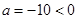 可知拋物線的開口向下,設成本為
可知拋物線的開口向下,設成本為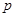 (元),再根據題意列出p關于x的函數關系式,再根據一次函數的性質即可求得結果.
(元),再根據題意列出p關于x的函數關系式,再根據一次函數的性質即可求得結果.
(1)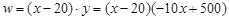 =
=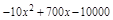
∵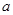 = -10<0,
= -10<0,
∴當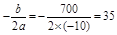 時,w可取得最大值.
時,w可取得最大值.
即當銷售單價定為35元時,每月可獲得最大利潤2250元;
(2)依題意得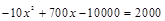 .
.
解得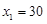 ,
,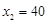 .
.
即如果此商店想要每月獲得2000元的利潤,那么銷售單價應定為30元或40元;
(3)∵ 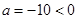 ,
,
∴ 拋物線的開口向下.
∴ 當30≤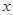 ≤40時,
≤40時,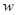 ≥2000.
≥2000.
∵ 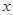 ≤32,
≤32,
∴ 30≤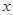 ≤32.
≤32.
設成本為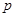 (元),依題意得
(元),依題意得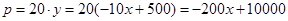 .
.
∵ 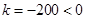 ,
,
∴ 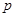 隨
隨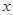 的增大而減小.
的增大而減小.
∴ 當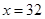 時,
時,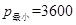 .
.
答:此商店想要每月獲得的利潤不低于2000元,每月的成本最少需要3600元.
考點:二次函數的應用
點評:二次函數的應用是初中數學的重點和難點,是中考常見題,一般難度不大.


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:
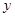 (件)與銷售單價
(件)與銷售單價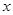 (元)之間的關系可近似的看作一次函數:
(元)之間的關系可近似的看作一次函數: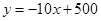 .
.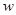 (元),當銷售單價定為多少元時,每月可獲得最大利潤?【利
(元),當銷售單價定為多少元時,每月可獲得最大利潤?【利 潤=(銷售單價-進價)×銷售量】
潤=(銷售單價-進價)×銷售量】查看答案和解析>>
科目:初中數學 來源:2011-2012年北京昌平區九年級第一學期期末考試數學卷 題型:解答題
某大學校園內一商店,銷售一種進價為每件20元的臺燈.銷售過程中發現,每月銷售量 (件)與銷售單價
(件)與銷售單價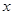 (元)之間的關系可近似的看作一次函數:
(元)之間的關系可近似的看作一次函數: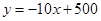 .
.
【小題1】(1)設此商店每月獲得利潤為 (元),當銷售單價定為多少元時,每月可獲得最大利潤?【利
(元),當銷售單價定為多少元時,每月可獲得最大利潤?【利 潤=(銷售單價-進價)×銷售量】
潤=(銷售單價-進價)×銷售量】
【小題2】(2)如果此商店想要每月獲得2000元的利潤,那么銷售單價應定為多少元?
【小題3】(3)根據物價部門規定,這種臺燈的銷售單價不得高于32元,如果此商店想要每月獲得的利潤不低于2000元,那么商店每月的成本最少需要多少元?【成本=進價×銷售量】
查看答案和解析>>
科目:初中數學 來源:2013屆江蘇省江陰市要塞中學上學期期末考試數學試卷(帶解析) 題型:解答題
某大學校園內一商店,銷售一種進價為每件20元的臺燈.銷售過程中發現,每月銷售量y(件)與銷售單價x(元)之間的關系可近似的看作一次函數: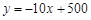 .
.
(1)設此商店每月獲得利潤為w(元),求w與x的函數關系式,并求出w的最大值;
(2)如果此商店想要每月獲得2000元的利潤,那么銷售單價應定為多少元?
(3)根據物價部門規定,這種臺燈的銷售單價不得高于32元,如果此商店想要每月獲得的利潤不低于2000元,那么商店每月的成本最少需要多少元?
查看答案和解析>>
科目:初中數學 來源:2011-2012年北京昌平區九年級第一學期期末考試數學卷 題型:解答題
某大學校園內一商店,銷售一種進價為每件20元的臺燈.銷售過程中發現,每月銷售量 (件)與銷售單價
(件)與銷售單價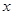 (元)之間的關系可近似的看作一次函數:
(元)之間的關系可近似的看作一次函數: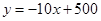 .
.
1.(1)設此商店每月獲得利潤為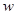 (元),當銷售單價定為多少元時,每月可獲得最大利潤?【利潤=(銷售單價-進價)×銷售量】
(元),當銷售單價定為多少元時,每月可獲得最大利潤?【利潤=(銷售單價-進價)×銷售量】
2.(2)如果此商店想要每月獲得2000元的利潤,那么銷售單價應定為多少元?
3.(3)根據物價部門規定,這種臺燈的銷售單價不得高于32元,如果此商店想要每月獲得的利潤不低于2000元,那么商店每月的成本最少需要多少元?【成本=進價×銷售量】
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com