
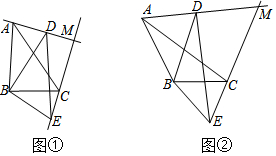
分析 (1)根據(jù)等腰三角形兩底角相等,即可解決問題.
(2)存在.首先證明∠AMC=90°,在Rt△ABC中,根據(jù)AB=4,BC=3,可得AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,可得S△ABC=$\frac{1}{2}$×3×4=6,因為當△ACM的面積最大時,四邊形ABCM的面積最大,因為△ACM是直角三角形,AC=5,所以當AM=CM=$\frac{5\sqrt{2}}{2}$時,△ACM的面積最大,最大值為=$\frac{25}{4}$,由此即可解決問題.
(3)存在.如圖②中,作AN⊥BC于N.首先證明∠AMC=60°,在Rt△ABN中,AB=4,∠ABN=60°,推出BN=$\frac{1}{2}$AB=2,AN=2$\sqrt{3}$,在Rt△ACN中,AC=$\sqrt{A{N}^{2}+C{N}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{5}^{2}}$=$\sqrt{37}$,可得S△ABC=$\frac{1}{2}$×3×2$\sqrt{3}$=3$\sqrt{3}$,因為當△ACM的面積最大時,四邊形ABCM的面積最大,因為∠AMC=60°所以當△ACM是等邊三角形時,△ACM的面積最大,由此即可解決問題.
解答 解:(1)∵BA=BD,∠ABD=30°,
∴∠BAD=∠BDA=$\frac{1}{2}$(180°-30°)=75°.
故答案為75°.
(2)存在.理由如下,
如圖①中,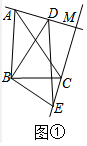
∵∠ABC=∠DBE,
∴∠ABD=∠CBE,
∵BA=BD,BC=BE,
∴∠BAD=∠BDA,∠BCE=∠BEC,
∴∠BCE=∠BAD,
∵∠BCE+∠BCM=180°,
∴∠BCM+∠BAM=180°,
∴∠ABC+∠AMC=180°,
∵∠ABC=90°,
∴∠AMC=90°,
在Rt△ABC中,∵AB=4,BC=3,
∴AC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵S△ABC=$\frac{1}{2}$×3×4=6,
∴當△ACM的面積最大時,四邊形ABCM的面積最大,
∵△ACM是直角三角形,AC=5,
∴當AM=CM=$\frac{5\sqrt{2}}{2}$時,△ACM的面積最大,最大值為=$\frac{25}{4}$,
∴四邊形ABCM的面積的最大值為$\frac{49}{4}$.
(3)存在.理由如下,
如圖②中,作AN⊥BC于N.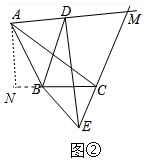
∵∠ABC=∠DBE,
∴∠ABD=∠CBE,
∵BA=BD,BC=BE,
∴∠BAD=∠BDA,∠BCE=∠BEC,
∴∠BCE=∠BAD,
∵∠BCE+∠BCM=180°,
∴∠BCM+∠BAM=180°,
∴∠ABC+∠AMC=180°,
∵∠ABC=120°,
∴∠AMC=60°,
在Rt△ABN中,∵AB=4,∠ABN=60°,
∴BN=$\frac{1}{2}$AB=2,AN=2$\sqrt{3}$,
在Rt△ACN中,AC=$\sqrt{A{N}^{2}+C{N}^{2}}$=$\sqrt{(2\sqrt{3})^{2}+{5}^{2}}$=$\sqrt{37}$
∴S△ABC=$\frac{1}{2}$×3×2$\sqrt{3}$=3$\sqrt{3}$,
∴當△ACM的面積最大時,四邊形ABCM的面積最大,
∵∠AMC=60°
∴當△ACM是等邊三角形時,△ACM的面積最大,最大值為=$\frac{\sqrt{3}}{4}$•AC2=$\frac{37\sqrt{3}}{4}$,
∴四邊形ABCM的面積的最大值為$\frac{49\sqrt{3}}{4}$.
點評 本題考查三角形綜合題、四邊形內(nèi)角和定理、勾股定理,三角形的面積等知識,解題的關(guān)鍵是證明∠AMC是特殊角,學(xué)會用轉(zhuǎn)化的思想思考問題,把求四邊形面積最大問題,轉(zhuǎn)化為求三角形面積最大問題,屬于中考壓軸題.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
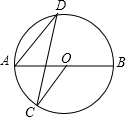 如圖,AB是⊙O的直徑,∠ADC的度數(shù)是35°,則∠BOC的度數(shù)是( )
如圖,AB是⊙O的直徑,∠ADC的度數(shù)是35°,則∠BOC的度數(shù)是( )| A. | 120° | B. | 110° | C. | 100° | D. | 70° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com