
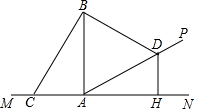
 如圖,在坡AP的坡腳A處豎有一根電線桿AB,為固定電線桿在地面C處和坡面D處各裝一根等長的引拉線BC和BD,過點D作地面MN的垂線DH,H為垂足,已知點C、A、H在一直線上,若測得AC=7米,AD=12米,坡角為30°,試求電線桿AB的高度;(精確到0.1米)
如圖,在坡AP的坡腳A處豎有一根電線桿AB,為固定電線桿在地面C處和坡面D處各裝一根等長的引拉線BC和BD,過點D作地面MN的垂線DH,H為垂足,已知點C、A、H在一直線上,若測得AC=7米,AD=12米,坡角為30°,試求電線桿AB的高度;(精確到0.1米) 分析 作BE⊥AD于點E,設AB=x米,在直角△ABE中,根據三角函數,利用x表示出AE和BE的長,則在直角△BED中,利用勾股定理表示出BD的長,在直角△ABC中利用勾股定理表示出BC,根據BC=BD即可列方程求解.
解答  解:作BE⊥AD于點E,設AB=x米,
解:作BE⊥AD于點E,設AB=x米,
在直角△ABE中,∠BAE=90°-∠DAH=90°-30°=60°,
則AE=AB•cos∠BAE=xcos60°=$\frac{1}{2}$x(米),
BE=AB•sin∠BAE=xsin60°=$\frac{\sqrt{3}}{2}$x(米).
則DE=AD-AE=12-$\frac{1}{2}$x,
在直角△BED中,BD2=BE2+DE2=($\frac{\sqrt{3}}{2}$x)2+(12-$\frac{1}{2}$x)2=144+x2-12x,
在直角△ABC中,BC2=AC2+AB2=72+x2=49+x2.
∵BC=BD,
∴144+x2-12x=49+x2.
解得x=$\frac{95}{12}$≈7.9
答:電線桿AB的高度約是7.9米.
點評 本題考查了解直角三角形的應用,坡度坡角問題,正確作出輔助線,利用AB的長表示抽BD和BC是關鍵.


科目:初中數學 來源: 題型:解答題
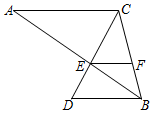 如圖,已知AC∥BD,AB和CD相交于點E,AC=6,BD=4,F是BC上一點,S△BEF:S△EFC=2:3.
如圖,已知AC∥BD,AB和CD相交于點E,AC=6,BD=4,F是BC上一點,S△BEF:S△EFC=2:3.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m•sinα | B. | m•cosα | C. | m•tanα | D. | m•cotα |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | y=4x2+2x+1 | B. | y=2x2-4x+1 | C. | y=2x2-x+4 | D. | y=x2-4x+2 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -$\frac{4}{5}$ | B. | -$\frac{5}{4}$ | C. | $\frac{5}{4}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | m=-3,n=2 | B. | m=3,n=2 | C. | m=-2,n=3 | D. | m=2,n=3 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,已知第一象限內的點A在反比例函數y=$\frac{2}{x}$上,第二象限內的點B在反比例函數y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\sqrt{2}$,則k的值為-4.
如圖,已知第一象限內的點A在反比例函數y=$\frac{2}{x}$上,第二象限內的點B在反比例函數y=$\frac{k}{x}$上,且OA⊥OB,tanA=$\sqrt{2}$,則k的值為-4.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com