
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)經過A(﹣1,0),B(4,0),C(0,2)三點
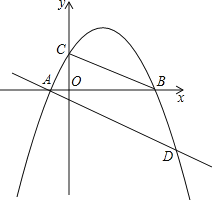
(1)求這條拋物線的解析式;
(2)E為拋物線上一動點,是否存在點E使以A、B、E為頂點的三角形與△COB相似?若存在,試求出點E的坐標;若不存在,請說明理由;
【答案】(1)、y=-![]() +
+![]() x+2;(2)、E點坐標為(0,2),(3,2).
x+2;(2)、E點坐標為(0,2),(3,2).
【解析】
試題分析:(1)、首先設出函數的解析式,然后利用待定系數法進行求解;(2)、首先根據題意判定△ABE只能是以點E為直角頂點的三角形,然后求出BC的長度,根據三角形相似求出點E的坐標.
試題解析:(1)、∵拋物線經過點C(0,2) ∴設該拋物線的解析式為y=a![]() +bx+2
+bx+2
將A、B兩點坐標代入解析式得:![]() 解得:
解得:
∴拋物線的解析式為:y=-![]() +
+![]() x+2
x+2
(2)、存在
由圖象可知,以A、B為直角頂點的△ABE不存在,所以△ABE只可能是以點E為直角頂點的三角形.
在Rt△BOC中,OC=2,OB=4, ∴BC=![]() =
=![]() .
.
在Rt△BOC中,設BC邊上的高為h,則![]() ×
×![]() h=
h=![]() ×2×4, ∴h=
×2×4, ∴h=![]() .
.
∵△BEA∽△COB,設E點坐標為(x,y), ∴![]() =
=![]() ,∴y=±2
,∴y=±2
將y=2代入拋物線y=-![]() +
+![]() x+2,得
x+2,得![]() =0,
=0,![]() =3.
=3.
當y=﹣2時,不合題意舍去.
∴E點坐標為(0,2),(3,2).



科目:初中數學 來源: 題型:
【題目】為了了解某縣七年級9800名學生的視力情況,從中抽查了100名學生的視力情況,就這個問題來說,下面說法正確的是( )
A. 9800名學生是總體 B. 每個學生是個體
C. 100名學生是所抽取的一個樣本 D. 樣本容量是100
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 的解析表達式為
的解析表達式為![]() ,且
,且![]() 與
與![]() 軸交于點
軸交于點![]() ,直線
,直線![]() 經過點
經過點![]() ,直線
,直線![]() ,
,![]() 交于點
交于點![]() .
.
(1)求點![]() 的坐標;(2)求直線
的坐標;(2)求直線![]() 的解析表達式;(3)求
的解析表達式;(3)求![]() 的面積;(4)在直線
的面積;(4)在直線![]() 上存在異于點
上存在異于點![]() 的另一點
的另一點![]() ,使得
,使得![]() 與
與![]() 的面積相等,請直接寫出點
的面積相等,請直接寫出點![]() 的坐標.
的坐標.
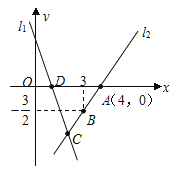
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠前年繳稅30萬元,今年繳稅36.3萬元,若該廠繳稅的年平均增長率為x,則可列方程( )
A.30x2=36.3
B.30(1-x)2=36.3
C.30+30(1+x)+30(1+x)2=36.3
D.30(1+x)2=36.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠MON=90°,點A、B分別在直線OM、ON上,BC是∠ABN的平分線.
(1)如圖1,若BC所在直線交∠OAB的平分線于點D時,嘗試完成①、②兩題:
①當∠ABO=30°時,∠ADB= °
②當點A、B分別在射線OM、ON上運動時(不與點O重合),試問:隨著點A、B的運動,∠ADB的大小會變嗎?如果不會,請求出∠ADB的度數;如果會,請求出∠ADB的度數的變化范圍;
(2)如圖2, 若BC所在直線交∠BAM的平分線于點C時,將△ABC沿EF折疊,使點C落在四邊形ABEF內點C′的位置.求∠BEC′+∠AFC′ 的度數.
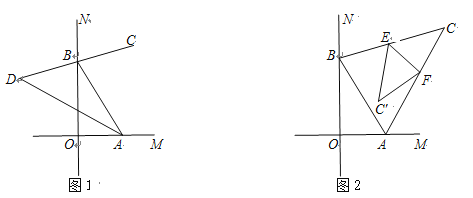
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com