
| A. | $\frac{\sqrt{3}}{8}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{8}$ |
分析 由于內(nèi)接正三角形、正方形、正六邊形是特殊內(nèi)角的多邊形,可構(gòu)造直角三角形分別求出邊心距的長,由勾股定理逆定理可得該三角形是直角三角形,進(jìn)而可得其面積.
解答 解:如圖1,
∵OC=1,
∴OD=1×sin30°=$\frac{1}{2}$;
如圖2,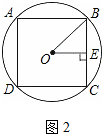
∵OB=1,
∴OE=1×sin45°=$\frac{\sqrt{2}}{2}$;
如圖3,
∵OA=1,
∴OD=1×cos30°=$\frac{\sqrt{3}}{2}$,
則該三角形的三邊分別為:$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$,
∵($\frac{1}{2}$)2+($\frac{\sqrt{2}}{2}$)2=($\frac{\sqrt{3}}{2}$)2,
∴該三角形是直角三角形,
∴該三角形的面積是$\frac{1}{2}$×$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{8}$,
故選:D.
點(diǎn)評 本題主要考查多邊形與圓,解答此題要明確:多邊形的半徑、邊心距、中心角等概念,根據(jù)解直角三角形的知識解答是解題的關(guān)鍵.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2cm | B. | 4cm | C. | 2cm或4cm | D. | 4cm或6cm |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
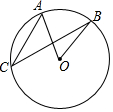 如圖,⊙O中,弦AC與BC時兩條弦,∠C=35°,則∠O的度數(shù)是( )
如圖,⊙O中,弦AC與BC時兩條弦,∠C=35°,則∠O的度數(shù)是( )| A. | 25° | B. | 35° | C. | 65° | D. | 70° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 向左平移1個單位,再向上平移1個單位 | |
| B. | 向右平移1個單位,再向下平移1個單位 | |
| C. | 向左平移1個單位,再向下平移1個單位 | |
| D. | 向右平移1個單位,再向上平移1個單位 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題

| A. | 66° | B. | 60° | C. | 56° | D. | 54° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com