
(本題滿分10分)在△ABC中,∠A=90°,點D在線段BC上,∠EDB= ∠C,BE⊥DE,垂足為E,DE與AB相交于點F.
∠C,BE⊥DE,垂足為E,DE與AB相交于點F.

(1)當AB=AC時,(如圖1),
①∠EBF= °
②探究線段BE與FD的數量關系,并加以證明;
(2)當AB=kAC時(如圖2),求 的值(用含k的式子表示).
的值(用含k的式子表示).
(1)①∠EBF=22.5°;②FD=2BE;(2) .
.
【解析】
試題分析:(1)①根據題意可判斷△ABC為等腰直角三角形,據此即可推斷∠C=45°,進而可知∠EDB=22.5°.然后求出∠EBF的度數.
②根據題意證明△BEF∽△DEB,然后利用相似三角形的性質,得到BE與FD的數量關系.
(2)首先證明△GBN∽△FDN,利用三角形相似的性質得到BE與FD的數量關系.
試題解析:(1)①∵AB=AC∠A=90°,∴∠ABC=∠C=45°,
∵∠EDB= ∠C,∴∠EDB=22.5°,∵BE⊥DE,∴∠EBD=67.5°,∴∠EBF=67.5°﹣45°=22.5°;
∠C,∴∠EDB=22.5°,∵BE⊥DE,∴∠EBD=67.5°,∴∠EBF=67.5°﹣45°=22.5°;
②在△BEF和△DEB中,∵∠BED=∠FEB=90°,∠EBF=∠EDB=22.5°,∴△BEF∽△DEB,
如圖:作BG平分∠ABC,交DE于G點,∴BG=GD,△BEG是等腰直角三角形,

設EF=x,BE=y,則:BG=GD= ,FD=
,FD= ,
,
∵△BEF∽△DEB,∴ ,即:
,即: ,得:
,得: ,
,
∴FD= ,∴FD=2BE.
,∴FD=2BE.
(2)過點D作DG∥AC,交BE的延長線于點G,與BA交于點N,
∵DG∥AC,∴∠GDB=∠C,
∵∠EDB= ∠C,∴∠EDB=∠GDE,
∠C,∴∠EDB=∠GDE,
∵BE⊥DE,∴∠BED=∠DEG,DE=DE,∴△DEG≌△DEB,
∴BE= GB,∠BND=∠GNB=90°,∠EBF=∠NDF,∴△GBN∽△FDN,
GB,∠BND=∠GNB=90°,∠EBF=∠NDF,∴△GBN∽△FDN,
∴ ,即
,即 ,
,
又∵DG∥AC,∴△BND∽△BAC,∴ ,即
,即 ,∴
,∴ .
.

考點:1.相似三角形的判定與性質;2.角平分線的性質;3.等腰直角三角形.


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:初中數學 來源:2014-2015學年江蘇省泰州市姜堰區八年級上學期期中考試數學試卷(解析版) 題型:選擇題
到三角形的三個頂點距離相等的點是( )
A.三條角平分線的交點
B.三條中線的交點
C.三條高的交點
D.三條邊的垂直平分線的交點
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省蘇州市高新區九年級上學期期中聯考數學試卷(解析版) 題型:填空題
如果函數 的圖象經過平面直角坐標系的四個象限,那么
的圖象經過平面直角坐標系的四個象限,那么 的取值范圍是 .
的取值范圍是 .
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省江陰市青陽片七年級上學期期中考試數學試卷 題型:填空題
有一個正六面體骰子,放在桌面上,將骰子沿如圖所示的順時針方向滾動,每滾動 算一次,則滾動第
算一次,則滾動第 次后,骰子朝下一面的點數是 .
次后,骰子朝下一面的點數是 .

查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省鎮江市丹徒區八年級10月調研數學試卷(解析版) 題型:解答題
(10分)已知:如圖, ∠1=∠2,∠3=∠4,點E在BD上,連結AE、CE,求證AE=CE.

查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇省鎮江市丹徒區八年級10月調研數學試卷(解析版) 題型:解答題
作圖題:(5′+5′+5′,共15分)
(1)如圖,已知∠AOB及點C、D兩點,請利用直尺和圓規作一點P,使得點P到射線OA、OB的距離相等,且P點到點C、D的距離也相等。
(2)利用方格紙畫出△ABC關于直線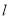 的對稱圖形△A′B′C′。
的對稱圖形△A′B′C′。
(3)如圖,已知在△ABC中,AB=AC ,AD是BC邊上的高,P是AB邊上的一點,試在高AD上找一點E,使得△PEB的周長最短。

查看答案和解析>>
科目:初中數學 來源:2014-2015學年河南平頂山第四十三中學七年級上第一次段考數學試卷(解析版) 題型:解答題
已知|a|=5,|b|=2,ab <0.求:3a +2b 的值 .
【解析】
∵|a|=5,∴a =_______.
∵|b|=2,∴b =_______.
∵ab <0,∴當a =_______時,b =_______,
當a =_______時,b=_______.
∴3a +2b =_______或3a +2b =_______.
∴3a +2b 的值為_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com