
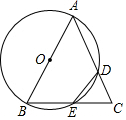
 如圖,在△ABC中,AB=AC,以AB為直徑的圓分別交邊AC,BC于點D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,則∠DEC的度數是( )
如圖,在△ABC中,AB=AC,以AB為直徑的圓分別交邊AC,BC于點D,E,若$\widehat{AD}$=$\widehat{DE}$+30°,則∠DEC的度數是( )| A. | 30° | B. | 40° | C. | 45° | D. | 50° |
分析 作輔助線,設∠EOD=x°,根據弧的度數即為弧所對圓心角的度數,分別表示出∠AOD、∠BOE的度數,再根據直徑所對的圓周角為直角和等腰三角形的三線合一得:AE是角平分線,即圓周角相等,則所對的弧相等,圓心角相等;根據平角的定義列方程可求x的值,最后由四點共圓的性質和同圓的半徑相等求出結論.
解答 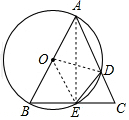 解:連接OE、OD、AE,
解:連接OE、OD、AE,
設∠EOD=x°,
∵$\widehat{AD}$=$\widehat{DE}$+30°,
∴∠AOD=(x+30)°,
∵AB為⊙O的直徑,
∴∠AEB=90°,
∵AB=AC,
∴∠BAE=∠CAE,
∴$\widehat{BE}$=$\widehat{ED}$,
∴∠BOE=x°,
則x+x+x+30=180,
x=50°,
∴∠AOD=30°+50°=80°,
∵OA=OD,
∴∠BAC=∠ADO=$\frac{180°-80°}{2}$=50°,
∵A、B、E、D四點共圓,
∴∠DEC=∠BAC=50°,
故選D.
點評 本題考查了弦、弧及圓心角的關系,圓周角定理,以及等腰三角形的性質,其中作出輔助線是解本題的關鍵,在圓中常作的輔助線是連接半徑,同時注意弧的度數即為弧所對圓心角的度數.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
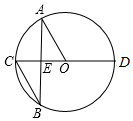 如圖,CD 是⊙O的直徑,A、B兩點在⊙O上,且 AB與CD交于點E,若∠BAO=30°,AO∥BC,則∠AOD的度數為( )
如圖,CD 是⊙O的直徑,A、B兩點在⊙O上,且 AB與CD交于點E,若∠BAO=30°,AO∥BC,則∠AOD的度數為( )| A. | 120° | B. | 100° | C. | 170° | D. | 150° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
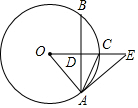 如圖,在⊙O中,OE垂直于弦AB,垂足為點D,交⊙O于點C,∠EAC=∠CAB.
如圖,在⊙O中,OE垂直于弦AB,垂足為點D,交⊙O于點C,∠EAC=∠CAB.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x1=0,x2=5 | B. | x1=1,x2=5 | C. | x1=1,x2=-5 | D. | x1=-1,x2=5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com