
【題目】如圖,射線OM上有三點A、B、C,滿足OA=20cm,AB=60cm,BC=10cm,點P從點O出發,沿OM方向以1cm/秒的速度勻速運動,點Q從點C出發在線段CO上向點O勻速運動,兩點同時出發,當點Q運動到點O時,點P、Q停止運動.
(1)若點Q運動速度為2cm/秒,經過多長時間P、Q兩點相遇?
(2)當P在線段AB上且PA=3PB時,點Q運動到的位置恰好是線段AB的三等分點,求點Q的運動速度;
![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】對于任意四個有理數a,b,c,d,可以組成兩個有理數對(a,b)與(c,d).我們規定:
(a,b)★(c,d)=bc﹣ad.
例如:(1,2)★(3,4)=2×3﹣1×4=2.
根據上述規定解決下列問題:
(1)有理數對(2,﹣3)★(3,﹣2)= ;
(2)若有理數對(﹣3,2x﹣1)★(1,x+1)=7,則x= ;
(3)當滿足等式(﹣3,2x﹣1)★(k,x+k)=5+2k的x是整數時,求整數k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在平面直角坐標系xOy中,已知點A(0,3),B(2,3),OC=a.將梯形ABCO沿直線y=x折疊,點A落在線段OC上,對應點為E.
(1)求點E的坐標;
(2)①若BC∥AE,求a的值;(提示:兩邊互相平行的四邊形是平行四邊形,平行四邊形的對邊相等)
②如圖②,若梯形ABCO的面積為2a,且直線y=mx將此梯形面積分為1∶2的兩部分,求直線y=mx的函數表達式.
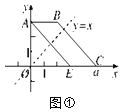
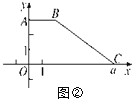
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一個口袋中裝有七個完全相同的小球,小球上分別標有-3、-2、-1、0、1、2、3七個數,攪勻后一次從中摸出一個小球,將小球上的數用![]() 表示,將
表示,將![]() 的值分別代入函數
的值分別代入函數![]() 和方程
和方程![]() ,恰好使得函數的圖像經過二、四象限,且方程有整數解,那么這7個數中所有滿足條件的
,恰好使得函數的圖像經過二、四象限,且方程有整數解,那么這7個數中所有滿足條件的![]() 的值之和是( )
的值之和是( )
A. 1 B. -1 C. -3 D. -4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在圖(1)中,對任意相鄰的上下或左右兩格中的數字同時加1或減2,這算作一次操作,經過若干次操作后,圖(1)能變為圖(2),則圖(2)中A格內的數是_____
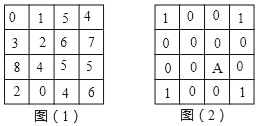
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,∠AOB和∠COD都是直角,
①若∠BOC=60°,則∠BOD= °,∠AOC= °;
②改變∠BOC的大小,則∠BOD與∠AOC相等嗎?為什么?
(2)如圖2,∠AOB=100°,∠COD=110°,若∠AOD=∠BOC+70°,求∠AOC的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某小區的一個健向器材,已知BC=0.15m,AB=2.70m,∠BOD=70°,求端點A到地面CD的距離(精確到0.1m).(參考數據:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知,BC∥OA,∠B=∠A=100°,試回答下列問題:
(1)如圖①,求證:OB∥AC. 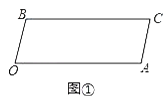
(2)如圖②,若點E、F在線段BC上,且滿足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度數. 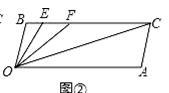
(3)在(2)的條件下,若平行移動AC,如圖③,那么∠OCB:∠OFB的值是否隨之發生變化?若變化,試說明理由;若不變,求出這個比值. 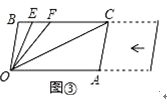
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com