Question

15．如圖，以長(zhǎng)方形ABCO中點(diǎn)O為原點(diǎn)，以O(shè)C，OA所在直線為x軸和y軸建立平面直角坐標(biāo)系，點(diǎn)A（0，a），C（b，0）滿足$\sqrt{a-2b}$+|b-2|=0．
（1）求點(diǎn)A，B和C的坐標(biāo)．
（2）已知坐標(biāo)軸上有兩動(dòng)點(diǎn)P，Q同時(shí)出發(fā)，P點(diǎn)從C點(diǎn)出發(fā)沿x軸負(fù)方向以1個(gè)單位長(zhǎng)度每秒的速度勻速移動(dòng)．Q點(diǎn)從O點(diǎn)出發(fā)以2個(gè)單位長(zhǎng)度每秒的速度沿O→A→B→C的路線移動(dòng)，點(diǎn)Q到達(dá)C點(diǎn)整個(gè)運(yùn)動(dòng)隨之結(jié)束．若長(zhǎng)方形對(duì)角線AC，BO的交點(diǎn)D的坐標(biāo)是（1，2），設(shè)運(yùn)動(dòng)時(shí)間為t（t＞0）秒．問：是否存在這樣的t，使S_△ODP=S_△ODQ？若存在，請(qǐng)求出t的值；若不存在，請(qǐng)說明理由；
（3）點(diǎn)F是線段AC上一點(diǎn)，滿足∠FOC=∠FCO，點(diǎn)G是第二象限中一點(diǎn)，連OG，使得∠AOG=∠AOF．點(diǎn)E是線段OA上一動(dòng)點(diǎn)，連CE交OF于點(diǎn)H，下列兩個(gè)結(jié)論：①$\frac{∠OHC-∠ACE}{∠OEC}$的值不變；②$\frac{∠OHC+∠ACE}{∠OEC}$的值不變，其中有且只有一個(gè)結(jié)論是正確的，請(qǐng)你找出正確的結(jié)論并求其值．

Answer 1

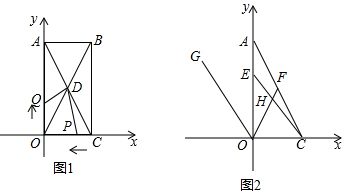
分析 （1）根據(jù)絕對(duì)值和算術(shù)平方根的非負(fù)性，求得a，b的值即可；
（2）①當(dāng)0＜t≤2時(shí)；②當(dāng)2≤t≤3時(shí)，③當(dāng)3≤t≤5時(shí)，再根據(jù)S_△ODP=S_△ODQ，列出關(guān)于t的方程，求得t的值即可；
（3）過H點(diǎn)作AC的平行線，交x軸于P，先判定OG∥AC，再根據(jù)角的和差關(guān)系以及平行線的性質(zhì)，得出∠PHO=∠GOF=∠1+∠2，∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4，最后代入$\frac{∠OHC+∠ACE}{∠OEC}$進(jìn)行計(jì)算即可．

解答 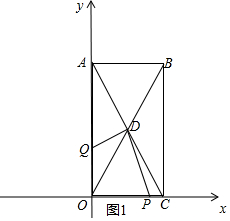解：（1）∵$\sqrt{a-2b}$+|b-2|=0，
∴a-2b=0，b-2=0，
解得a=4，b=2，
∴A（0，4），C（2，0），
∵AB∥x軸，BC∥y軸，
∴B（2，4）；

（2）由條件可知：P點(diǎn)從C點(diǎn)運(yùn)動(dòng)到O點(diǎn)時(shí)間為2秒，Q點(diǎn)從O點(diǎn)運(yùn)動(dòng)到A點(diǎn)時(shí)間為2秒，
①當(dāng)0＜t≤2時(shí)，點(diǎn)Q在線段AO上，
即 CP=t，OP=2-t，OQ=2t，AQ=4-2t，
∴S_△DOP=$\frac{1}{2}$OP•y_D=$\frac{1}{2}$（2-t）×2=2-t，
∵S_△ODP=S_△ODQ，
∴2-t=t，
∴t=1；
②當(dāng)2≤t≤3時(shí)，點(diǎn)Q在線段AB上，即CP=t，OP=t-2，QB=6-2t，
S_△DOP=$\frac{1}{2}$OP•y_D=$\frac{1}{2}$（t-2）×2=t-2，
S_△DOP=S_△OBQ-S_△DBQ=$\frac{1}{2}$QB•AO-$\frac{1}{2}$QB（y_B-y_D）=$\frac{1}{2}$×（6-2t）×4-$\frac{1}{2}×$（6-2t）（4-2）=6-2t，
∵S_△DOQ=S_△ODQ，
∴t-2=6-2t，
∴t=$\frac{8}{3}$；
③當(dāng)3≤t≤5時(shí)，點(diǎn)Q在線段BC上，CP=t，OP=t-2，QB=2t-6，
S_△DOP=$\frac{1}{2}$OP•y_D=$\frac{1}{2}$（t-2）×=t-2，
S_△DOQ=S_△OBQ-S_△DBQ=$\frac{1}{2}$QB•OC-$\frac{1}{2}$QB（x_B-x_D）=$\frac{1}{2}$×（2t-6）-$\frac{1}{2}$（6-2t）（2-1）=t-3，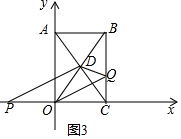
∵S_△ODP=S_△ODQ，
∴t-2=t-3，無解，
此情況下不存在這樣的t，
∴當(dāng)t=1或t=$\frac{8}{3}$時(shí)，S_△ODP=S_△ODQ；


（3）$\frac{∠OHC+∠ACE}{∠OEC}$的值不變，其值為2．
∵∠2+∠3=90°，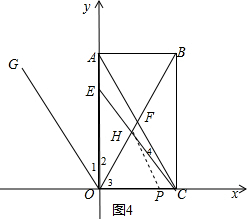
又∵∠1=∠2，∠3=∠FCO，
∴∠GOC+∠ACO=180°，
∴OG∥AC，
∴∠1=∠CAO，
∴∠OEC=∠CAO+∠4=∠1+∠4，
如圖，過H點(diǎn)作AC的平行線，交x軸于P，則∠4=∠PHC，PH∥OG，
∴∠PHO=∠GOF=∠1+∠2，
∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4，
∴$\frac{∠OHC+∠ACE}{∠OEC}$=$\frac{∠1+∠2+∠4+∠4}{∠1+∠4}$=$\frac{2（∠1+∠4）}{∠1+∠4}$=2．

點(diǎn)評(píng) 本題主要考查了坐標(biāo)與圖形性質(zhì)，解決問題的關(guān)鍵值作輔助線構(gòu)造平行線．解題時(shí)注意：任意一個(gè)數(shù)的絕對(duì)值都是非負(fù)數(shù)，算術(shù)平方根具有非負(fù)性，非負(fù)數(shù)之和等于0時(shí)，各項(xiàng)都等于0．