
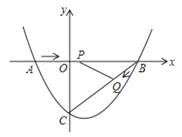
【題目】如圖,在平面直角坐標系中,拋物線y =ax2+bx﹣3(a≠0)與x軸交于點A(﹣2,0)、B(4,0)兩點,與y軸交于點C.點P、Q分別是AB、BC上的動點,當點P從A點出發,在線段AB上以每秒3個單位長度的速度向B點運動,同時點Q從B點出發,在線段BC上以每秒1個單位長度的速度向C點運動,其中一個點到達終點時,另一個點也停止運動.設P、Q同時運動的時間為t秒(0<t<2).
(1)求拋物線的表達式;
(2)設△PBQ的面積為S ,當t為何值時,△PBQ的面積最大,最大面積是多少?
(3)當t為何值時,△PBQ是等腰三角形?
【答案】(1)y=![]() x2
x2![]() x3;(2)當t=1時,S△PBQ最大=
x3;(2)當t=1時,S△PBQ最大=![]() .;(3)當t的值是
.;(3)當t的值是![]() 秒或
秒或![]() 秒或
秒或![]() 秒時,△CPQ為等腰三角形.
秒時,△CPQ為等腰三角形.
【解析】(1)把點A、B的坐標分別代入拋物線解析式,列出關于系數a、b的解析式,通過解方程組求得它們的值;
(2)設運動時間為t秒.利用三角形的面積公式列出S△PBQ與t的函數關系式S△PBQ=-![]() (t-1)2+
(t-1)2+![]() .利用二次函數的圖象性質進行解答;
.利用二次函數的圖象性質進行解答;
(3)分為三種情況:①當PB=BQ,②當PQ=BQ,③當PQ=PB進行討論,
(1)把點A(2,0)、B(4,0)分別代入y=ax2+bx3(a≠0),得
![]()
解得a=![]() ,b=
,b=![]()
所以該拋物線的表達式式為:y=![]() x2
x2![]() x3
x3
(2)由題意可知:AP=3t,BQ=t.
∴PB=63t.
由題意得,點C的坐標為(0,3).
在Rt△BOC中,BC=![]() .
.
如圖1,過點Q作QH⊥AB于點H.
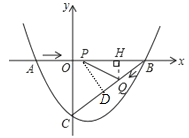
∴QH∥CO,
∴△BHQ∽△BOC
∴![]() ,即
,即![]()
∴HQ=![]() t.
t.
∴S△PBQ=![]() PBHQ=
PBHQ=![]() (63t)
(63t) ![]() t=
t=![]() t2+
t2+![]()
t=![]() (t1)2+
(t1)2+![]() .
.
∴當t=1時,S△PBQ最大=![]() . ()
. ()
答:運動1秒使△PBQ的面積最大,最大面積是![]() ;
;
(3)分為三種情況:①當PB=BQ時,即63t=t,解得t=![]()
當t=![]() 秒,△BPQ是等腰三角形。
秒,△BPQ是等腰三角形。
②當PQ=BQ時,
∵QH⊥PB,
∴PH=BH=![]() (63t)=3
(63t)=3![]() t,
t,
∵cos∠HBQ=![]()
∴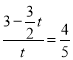 ,解得t=
,解得t=![]()
∴當t=![]() 秒時,△BPQ是等腰三角形,
秒時,△BPQ是等腰三角形,
③當PQ=PB時,如圖,過P點作PD⊥BC
∵PD⊥BC,
∴BD=QD=![]() BQ=
BQ=![]() t,
t,
∵cos∠HBQ=![]()
∴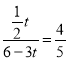 ,解得t=
,解得t=![]()
∴當t=![]() 秒時,△CPQ是等腰三角形,
秒時,△CPQ是等腰三角形,
即當△CPQ為等腰三角形時,t的值是![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.


科目:初中數學 來源: 題型:
【題目】“五一”期間,小明一家乘坐高鐵前往某市旅游,計劃第二天租用新能源汽車自駕出游。
 [來
[來
根據以上信息,解答下列問題:
(1)設租車時間為![]() 小時,租用甲公司的車所需費用為
小時,租用甲公司的車所需費用為![]() 元,租用乙公司的車所需費用為
元,租用乙公司的車所需費用為![]() 元,分別求出
元,分別求出![]() ,
,![]() 關于
關于![]() 的函數表達式;
的函數表達式;
(2)請你幫助小明計算并選擇哪個出游方案合算。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小麗和小華想利用摸球游戲決定誰去參加市里舉辦的書法比賽,游戲規則是:在一個不透明的袋子里裝有除數字外完全相同的4個小球,上面分別標有數字2,3,4,5.一人先從袋中隨機摸出一個小球,另一人再從袋中剩下的3個小球中隨機摸出一個小球.若摸出的兩個小球上的數字和為偶數,則小麗去參賽;否則小華去參賽.
(1)用列表法或畫樹狀圖法,求小麗參賽的概率.
(2)你認為這個游戲公平嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上,張老師舉了以下的例題:
例1等腰三角形ABC中,![]() ,求
,求![]() 的度數.(答案:35°)
的度數.(答案:35°)
例2等腰三角形ABC中,![]() ,求
,求![]() 的度數.(答案:40°或70°或100°)
的度數.(答案:40°或70°或100°)
張老師啟發同學們編題,小剛編了如下一題:
(1)等腰三角形ABC中,![]() ,則
,則![]() 的度數為______;(2)小剛發現,
的度數為______;(2)小剛發現,![]() 的度數不同,得到
的度數不同,得到![]() 的度數的個數也可能不同.如果在等腰三角形ABC中,設
的度數的個數也可能不同.如果在等腰三角形ABC中,設![]() ,當
,當![]() 有三個不同的度數時,x的取值范圍是______.
有三個不同的度數時,x的取值范圍是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
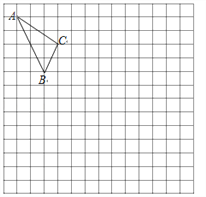
【題目】在如圖的正方形網格中,每一個小正方形的邊長為1.格點三角形![]() (頂點是網格線交點的三角形)的頂點
(頂點是網格線交點的三角形)的頂點![]() 的坐標分別是
的坐標分別是![]() .
.
(1)請在圖中的網格平面內建立平面直角坐標系;
(2)請畫出![]() 關于
關于![]() 軸對稱的
軸對稱的![]() ;
;
(3)請在![]() 軸上求作一點
軸上求作一點![]() ,使
,使![]() 的周長最小,并寫出點
的周長最小,并寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
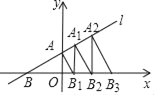
【題目】如圖,在平面直角坐標系中,直線l:y=![]() x+1交x軸于點B,交y軸于點A,過點A作AB1⊥AB交x軸于點B1,過點B1作B1A1⊥x軸交直線l于點A2…依次作下去,則點Bn的橫坐標為_____.
x+1交x軸于點B,交y軸于點A,過點A作AB1⊥AB交x軸于點B1,過點B1作B1A1⊥x軸交直線l于點A2…依次作下去,則點Bn的橫坐標為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2﹣9ax+18a的圖象與x軸交于A,B兩點(A在B的左側),圖象的頂點為C,直線AC交y軸于點D.
(1)連接BD,若∠BDO=∠CAB,求這個二次函數的表達式;
(2)是否存在以原點O為對稱軸的矩形CDEF?若存在,求出這個二次函數的表達式,若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com