
分析 (1)首先根據總價=單價×數量,求出太陽花的付款金額y(元)關于購買量x(盆)的函數解析式;然后分兩種情況:①一次購買的繡球花不超過20盆;②一次購買的繡球花超過20盆;根據總價=單價×數量,求出繡球花的付款金額y(元)關于購買量x(盆)的函數解析式即可.
(2)首先太陽花數量不超過繡球花數量的一半,可得太陽花數量不超過兩種花數量的$\frac{1}{3}$,即太陽花數量不超過30盆,所以繡球花的數量不少于60盆;然后設太陽花的數量是x盆,則繡球花的數量是90-x盆,根據總價=單價×數量,求出購買兩種花的總費用是多少,進而判斷出兩種花卉各買多少盆時,總費用最少,最少費用是多少元即可.
解答 解:(1)太陽花的付款金額y(元)關于購買量x(盆)的函數解析式是:y=6x;
①一次購買的繡球花不超過20盆時,
付款金額y(元)關于購買量x(盆)的函數解析式是:y=10x(x≤20);
②一次購買的繡球花超過20盆時,
付款金額y(元)關于購買量x(盆)的函數解析式是:
y=10×20+10×0.8×(x-20)
=200+8x-160
=8x+40
綜上,可得
繡球花的付款金額y(元)關于購買量x(盆)的函數解析式是:
y=$\left\{\begin{array}{l}{10x,(x≤20)}\\{8x+40,(x>20)}\end{array}\right.$
(2)根據題意,可得太陽花數量不超過:90×$\frac{1}{3}$,
所以繡球花的數量不少于:90-30=60(盆),
設太陽花的數量是x盆,則繡球花的數量是90-x盆,購買兩種花的總費用是y元,
則x≤30,
則y=6x+[8(90-x)+40]
=6x+[760-8x]
=760-2x
因為x≤30,
所以當x=30時,
ymin=760-2×30=700(元),
即太陽花30盆,繡球花60盆時,總費用最少,最少費用是700元.
答:太陽花30盆,繡球花60盆時,總費用最少,最少費用是700元.
點評 (1)此題主要考查了一次函數解析式的求法,以及一次函數的最值的求法,要熟練掌握,解答此題的關鍵是要明確:分段函數是在不同區間有不同對應方式的函數,要特別注意自變量取值范圍的劃分,既要科學合理,又要符合實際.
(2)此題還考查了單價、總價、數量的關系:總價=單價×數量,單價=總價÷數量,數量=總價÷單價,要熟練掌握.


 學練快車道快樂假期寒假作業系列答案
學練快車道快樂假期寒假作業系列答案科目:初中數學 來源: 題型:解答題
 如圖,拋物線y=ax2-x-$\frac{3}{2}$與x軸正半軸交于點A(3,0).以OA為邊在x軸上方作正方形OABC,延長CB交拋物線于點D,再以BD為邊向上作正方形BDEF.求a的值和點E的坐標.
如圖,拋物線y=ax2-x-$\frac{3}{2}$與x軸正半軸交于點A(3,0).以OA為邊在x軸上方作正方形OABC,延長CB交拋物線于點D,再以BD為邊向上作正方形BDEF.求a的值和點E的坐標.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
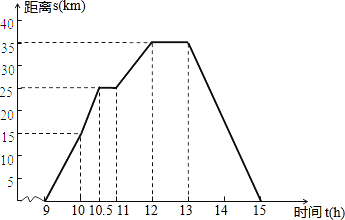 小明在某周末上午9時騎自行車離開家去綠道鍛煉,15時回家,已知自行車離家的距離s(km)與時間t(h)之間的關系如圖所示.根據圖象回答下列問題:
小明在某周末上午9時騎自行車離開家去綠道鍛煉,15時回家,已知自行車離家的距離s(km)與時間t(h)之間的關系如圖所示.根據圖象回答下列問題:查看答案和解析>>
科目:初中數學 來源: 題型:填空題
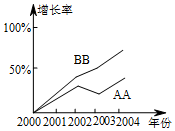 如圖,是兩種品牌的方便面銷售增長率折線統計圖,則AA牌方便面2003年的銷售量低于2002年的銷售量,2002年BB牌方便面的銷售量高于AA牌方便面的銷售量(填“高于”“低于”“不一定高于”)
如圖,是兩種品牌的方便面銷售增長率折線統計圖,則AA牌方便面2003年的銷售量低于2002年的銷售量,2002年BB牌方便面的銷售量高于AA牌方便面的銷售量(填“高于”“低于”“不一定高于”)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com