
【題目】(8分)如圖,AC是ABCD的一條對角線,過AC中點O的直線分別交AD,BC于點E,F.
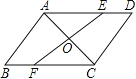
(1)求證:△AOE≌△COF;
(2)當EF與AC滿足什么條件時,四邊形AFCE是菱形?并說明理由.
【答案】(1)參見解析;(2)EF⊥AC時,四邊形AFCE是菱形.
【解析】
試題(1)由平行四邊形的性質得出AD∥BC,得出∠EAO=∠FCO,利用對頂角相等∠AOE=∠COF,O是AC的中點,OA=OC,所以由ASA即可得出結論;(2)此題應用菱形的判定,先說明四邊形AFCE已經是平行四邊形,再應用對角線互相垂直的平行四邊形是菱形即可.由△AOE≌△COF,得出對應邊相等AE=CF,證出四邊形AFCE是平行四邊形,再由對角線EF⊥AC,即可得出四邊形AFCE是菱形.
試題解析:(1)∵四邊形ABCD是平行四邊形,∴AD∥BC,∴∠EAO=∠FCO,∵O是CA的中點,∴OA=OC,又∵∠AOE=∠COF(對頂角相等),∴△AOE≌△COF(ASA);(2)∵△AOE≌△COF,∴AE=CF,∵AE∥CF,∴四邊形AFCE是平行四邊形(一組對邊平行且相等的四邊形是平行四邊形),當EF⊥AC時四邊形AFCE是菱形(對角線互相垂直的平行四邊形是菱形),∴EF⊥AC時,四邊形AFCE是菱形.


 智能訓練練測考系列答案
智能訓練練測考系列答案 計算高手系列答案
計算高手系列答案科目:初中數學 來源: 題型:
【題目】菜農李偉種植的某蔬菜計劃以每千克![]() 元的單價對外批發銷售,由于部分菜農盲目擴大種植,造成該蔬菜滯銷.李偉為了加快銷售,減少損失,對價格經過兩次下調后,以每千克
元的單價對外批發銷售,由于部分菜農盲目擴大種植,造成該蔬菜滯銷.李偉為了加快銷售,減少損失,對價格經過兩次下調后,以每千克![]() 元的單價對外批發銷售.
元的單價對外批發銷售.
![]() 求平均每次下調的百分率;
求平均每次下調的百分率;
![]() 小華準備到李偉處購買
小華準備到李偉處購買![]() 噸該蔬菜,因數量多,李偉決定再給予兩種優惠方案以供選擇:
噸該蔬菜,因數量多,李偉決定再給予兩種優惠方案以供選擇:
方案一:打九折銷售;
方案二:不打折,每噸優惠現金![]() 元.
元.
試問小華選擇哪種方案更優惠,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解學生課余活動情況.晨光中學對參加繪畫,書法,舞蹈,樂器這四個課外興趣小組的人員分布情況進行調査.并報據收集的數據繪制了兩幅不完整的統計閣.請根據圖中提供的信息.解答下面的問題:
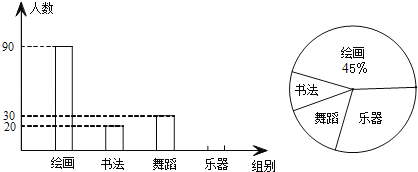
(1)此次共調查了多少名同學?
(2)將條形圖補充完整,并計算扇形統計圖中書法部分的圓心角的度數.
(3)如果該校共有300名學生參加這4個課外興趣小組,而每位教師最多只能輔導本組的20名學生,估計樂器興趣小組至少需要準備多少名教師?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中,∠ABC=90°,以AB為直徑作⊙O,點D為⊙O上一點,且CD=CB、連接DO并延長交CB的延長線于點E.
(1)判斷直線CD與⊙O的位置關系,并說明理由;
(2)若BE=4,DE=8,求AC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 年
年![]() 月,振華中學舉行了迎國慶中華傳統文化節活動.本次文化節共有五個活動:
月,振華中學舉行了迎國慶中華傳統文化節活動.本次文化節共有五個活動:![]() 書法比賽;
書法比賽;![]() 國畫競技;
國畫競技;![]() 詩歌朗誦;
詩歌朗誦;![]() 漢字大賽;
漢字大賽;![]() 古典樂器演奏.活動結束后,某班數學興趣小組開展了“我最喜愛的活動”的抽樣調查(每人只選一項),根據收集的數據繪制了兩幅不完整的統計圖,請根據圖中信息,解答下列問題:
古典樂器演奏.活動結束后,某班數學興趣小組開展了“我最喜愛的活動”的抽樣調查(每人只選一項),根據收集的數據繪制了兩幅不完整的統計圖,請根據圖中信息,解答下列問題:
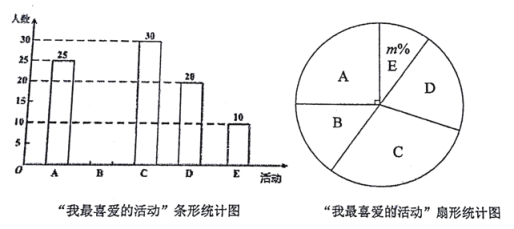
(1)此次催記抽取的初三學生共 人,![]() ,并補全條形統計圖;
,并補全條形統計圖;
(2)初三年級準備在五名優秀的書法比賽選手中任意選擇兩人參加學校的最終決賽,這五名選手中有三名男生和兩名女生,用樹狀圖或列表法求選出的兩名選手正好是一男一女的概率是多少.
查看答案和解析>>
科目:初中數學 來源: 題型:
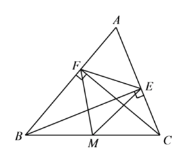
【題目】如圖,在△ABC中,CF⊥AB于點F,BE⊥AC于點E,M為BC的中點連接ME、MF、EF.
(1) 求證:△MEF是等腰三角形;
(2) 若∠A=![]() ,∠ABC=50°,求∠EMF的度數.
,∠ABC=50°,求∠EMF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校八年級學生進行了一次視力調查,繪制出頻數分布表和頻數直方圖的一部分如下:
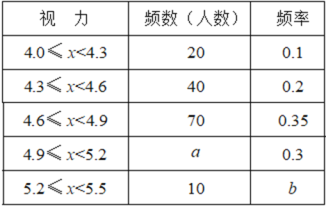
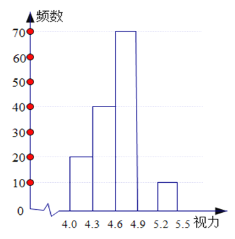
請根據圖表信息完成下列各題:
(1)在頻數分布表中,![]() 的值為 ,
的值為 ,![]() 的值是 ;
的值是 ;
(2)將頻數直方圖補充完整;
(3)小芳同學說“我的視力是此次調查所得數據的中位數”,你覺得小芳同學的視力應在哪個范圍內?
(4)若視力在不小于4.9的均屬正常,請你求出視力正常的人數占被調查人數的百分比.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司到果品基地購買某種優質水果慰問醫務工作者,果品基地對購買量在3000kg以上(含3000kg)的顧客采用兩種銷售方案.甲方案:每千克9元,由基地送貨上門;乙方案:每千克8元,由顧客自己租車運回.已知該公司租車從基地到公司的運輸費用為5000元.
(1)分別寫出該公司兩種購買方案付款金額y(元)與所購買的水果量x(kg)之間的函數關系式.
(2)當購買量在哪一范圍時,選擇哪種購買方案付款最少?并說明理由
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com