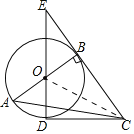
【題目】如圖，Rt△ABC中，∠ABC=90°，以AB為直徑作⊙O，點D為⊙O上一點，且CD=CB、連接DO并延長交CB的延長線于點E．
（1）判斷直線CD與⊙O的位置關系，并說明理由；
（2）若BE=4，DE=8，求AC的長．
【答案】（1）相切，證明見解析；（2）6
.
【解析】
（1）欲證明CD是切線，只要證明OD⊥CD，利用全等三角形的性質(zhì)即可證明；
（2）設⊙O的半徑為r．在Rt△OBE中，根據(jù)OE2=EB2+OB2，可得（8﹣r）2=r2+42，推出r=3，由tan∠E=
，推出
，可得CD=BC=6，再利用勾股定理即可解決問題.
（1）相切，理由如下，
如圖，連接OC，
∵CB=CD，CO=CO，OB=OD，
∴△OCB≌△OCD，
∴∠ODC=∠OBC=90°，
∴OD⊥DC，
∴DC是⊙O的切線；
（2）設⊙O的半徑為r，
在Rt△OBE中，∵OE2=EB2+OB2，
∴（8﹣r）2=r2+42，
∴r=3，AB=2r=6，
∵tan∠E=，
∴，
∴CD=BC=6，
在Rt△ABC中，AC=
．
科目：初中數(shù)學 來源： 題型：
【題目】如圖，
為
中的一條射線，點
在邊
上，
于
，交于點
，
交于點
，
于點
，
交
于點
，連接
交
于點
．
求證：四邊形
為矩形；
若
，試探究與
的數(shù)量關系，并說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知點A（―3，6）、B（―9，一3），以原點O為位似中心，相似比為
，把△ABO縮小，則點A的對應點A′的坐標是（ ）
A．（―1，2）
B．（―9，18）
C．（―9，18）或（9，―18）
D．（―1，2）或（1，―2）
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】閱讀理解：如圖
，在四邊形
的邊
上任取一點
（點不與
、
重合），分別連接
、
，可以把四邊形分成三個三角形，如果其中有兩個三角形相似，我們就把叫做四邊形的邊上的“相似點”：如果這三個三角形都相似，我們就把叫做四邊形的邊上的“強相似點”．解決問題：
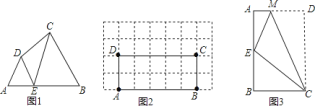
如圖，
，試判斷點是否是四邊形的邊上的相似點，并說明理由；
如圖
，在矩形中，、、
、
四點均在正方形網(wǎng)格（網(wǎng)格中每個小正方形的邊長為）的格點（即每個小正方形的頂點）上，試在圖②中畫出矩形的邊上的強相似點；
如圖
，將矩形沿
折疊，使點落在邊上的點處，若點恰好是四邊形
的邊上的一個強相似點，試探究與
的數(shù)量關系．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖，在直角坐標系中，先描出點
，點
.
（1）描出點
關于
軸的對稱點
的位置，寫出的坐標 ；
（2）用尺規(guī)在軸上找一點
，使
的值最小（保留作圖痕跡）；
（3）用尺規(guī)在軸上找一點
，使
（保留作圖痕跡）.
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】如圖△ABC內(nèi)接于⊙O，∠B=60°，CD是⊙O的直徑，點P是CD延長線上一點，且AP=AC．
（1）求證：PA是⊙O的切線；
（2）若PD=
，求⊙O的直徑．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
【題目】在Rt△ABC中，∠ACB=90°，∠A=30°，BD是△ABC的角平分線， DE⊥AB于點E．
（1）如圖1，連接EC，求證：△EBC是等邊三角形；
（2）點M是線段CD上的一點（不與點C，D重合），以BM為一邊，在BM的下方作∠BMG=60°，MG交DE延長線于點G．請你在圖2中畫出完整圖形，并直接寫出MD，DG與AD之間的數(shù)量關系；
（3）如圖3,點N是線段AD上的一點，以BN為一邊，在BN的下方作∠BNG=60°，NG交DE延長線于點G，且MB=MG．試探究ND，DG與AD數(shù)量之間的關系，并說明理由．
查看答案和解析>>
科目：初中數(shù)學 來源： 題型：
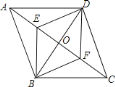
【題目】如圖，
是菱形
的對角線
、
的交點，
、
分別是
、
的中點．下列結(jié)論：①
；②四邊形
也是菱形；③四邊形的面積為
；④
；⑤
是軸對稱圖形．其中正確的結(jié)論有（ ）
A. 5個 B. 4個 C. 3個 D. 2個
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
