
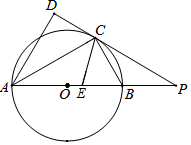
 如圖,AB是⊙O的直徑,點C是⊙O上一點,AD與過點C的切線垂直,垂足為點D,直線DC與AB的延長線相交于點P,CE平分∠ACB,交AB于點E.
如圖,AB是⊙O的直徑,點C是⊙O上一點,AD與過點C的切線垂直,垂足為點D,直線DC與AB的延長線相交于點P,CE平分∠ACB,交AB于點E.分析 (1)依據切線的性質可知OC⊥DC,然后可證明AD∥OC,依據平行線的性質可得到∠DAC=∠ACO,然后依據OA=OC可證明∠OAC=∠ACO,通過等量代換可證明AC平分∠DAB;
(2)依據直徑所對的圓周角等于90°可證明∠ACB=90°,然后依據同角的余角相等可證明∠DAC=∠BCP,由(1)可知AC平分∠DAB,從而得到∠CAE=∠BCP,然后結合∠ACE=∠ECB可證明∠PCE=∠PEC.
解答 解:(1)如圖1所示:連接OC.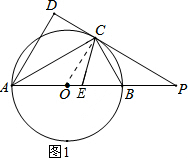
∵PD切⊙O于點C,
∴OC⊥PD.
又∵AD⊥PD,
∴OC∥AD.
∴∠ACO=∠DAC.
又∵OC=OA,
∴∠ACO=∠CAO,
∴∠DAC=∠CAO,
即AC平分∠DAB.
(2)∵AD⊥PD,
∴∠DAC+∠ACD=90°.
又∵AB為⊙O的直徑,
∴∠ACB=90°.
∴∠PCB+∠ACD=90°,
∴∠DAC=∠PCB.
又∵∠DAC=∠CAO,
∴∠CAO=∠PCB.
∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴∠CAO+∠ACE=∠PCB+∠BCE,
∴∠PEC=∠PCE,
∴PC=PE,
即△PCE是等腰三角形.
點評 本題主要考查的是切線的性質、圓周角定理的應用,等腰三角形的性質、三角形外角的性質,掌握有關切線問題的輔助線的作法是解題的關鍵.


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:初中數學 來源: 題型:選擇題
| A. | 由向左平移3個單位,再向上平移2個單位 | |
| B. | 由向右平移3個單位,再向下平移2個單位 | |
| C. | 由向右平移3個單位,再向上平移2個單位 | |
| D. | 由向左平移3個單位,再向下平移2個單位 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點O是△ABC內的一點,AB=AC,∠BAC=90°,∠BOC=120°,將△AOB繞點A按逆時針方向旋轉90°得到△ADC,連結OD.
如圖,點O是△ABC內的一點,AB=AC,∠BAC=90°,∠BOC=120°,將△AOB繞點A按逆時針方向旋轉90°得到△ADC,連結OD.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2x=196+4(70-x) | B. | 4x+2(70-x)=196 | C. | 2x+4(70-x)=196 | D. | 2x+196=4(70-x) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
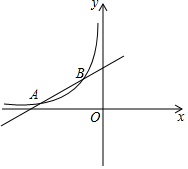 如圖,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函數y=kx+b與反比例函數y=$\frac{m}{x}$(m<0)圖象的兩個交點,求反比例函數的解析式,并根據圖象直接回答:在第二象限內,當x取何值時,一次函數的值大于反比例函數的值?
如圖,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函數y=kx+b與反比例函數y=$\frac{m}{x}$(m<0)圖象的兩個交點,求反比例函數的解析式,并根據圖象直接回答:在第二象限內,當x取何值時,一次函數的值大于反比例函數的值?查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com