
 如圖,∠ABC=∠ACB,AD、BD、CD分別平分△ABC的外角∠EAC、內(nèi)角∠ABC、外角∠ACF.以下結(jié)論:
如圖,∠ABC=∠ACB,AD、BD、CD分別平分△ABC的外角∠EAC、內(nèi)角∠ABC、外角∠ACF.以下結(jié)論:| A. | 2個(gè) | B. | 3個(gè) | C. | 4個(gè) | D. | 1 個(gè) |
分析 ①由AD平分△ABC的外角∠EAC,求出∠EAD=∠DAC,由三角形外角得∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,得出∠EAD=∠ABC,利用同位角相等兩直線平行得出結(jié)論正確.
②由AD∥BC,得出∠ADB=∠DBC,再由BD平分∠ABC,所以∠ABD=∠DBC,∠ABC=2∠ADB,得出結(jié)論∠ACB=2∠ADB,
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,利用角的關(guān)系得∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,得出結(jié)論∠ADC=90°-∠ABD;④由∠BAC+∠ABC=∠ACF,得出$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ACF,再與∠BDC+∠DBC=$\frac{1}{2}$∠ACF相結(jié)合,得出$\frac{1}{2}$∠BAC=∠BDC,即∠BDC=$\frac{1}{2}$∠BAC.
解答 解:①∵AD平分△ABC的外角∠EAC,
∴∠EAD=∠DAC,
∵∠EAC=∠ACB+∠ABC,且∠ABC=∠ACB,
∴∠EAD=∠ABC,
∴AD∥BC,
故①正確.
②由(1)可知AD∥BC,
∴∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠ABC=2∠ADB,
∵∠ABC=∠ACB,
∴∠ACB=2∠ADB,
故②正確.
③在△ADC中,∠ADC+∠CAD+∠ACD=180°,
∵CD平分△ABC的外角∠ACF,
∴∠ACD=∠DCF,
∵AD∥BC,
∴∠ADC=∠DCF,∠ADB=∠DBC,∠CAD=∠ACB
∴∠ACD=∠ADC,∠CAD=∠ACB=∠ABC=2∠ABD,
∴∠ADC+∠CAD+∠ACD=∠ADC+2∠ABD+∠ADC=2∠ADC+2∠ABD=180°,
∴∠ADC+∠ABD=90°
∴∠ADC=90°-∠ABD,
故③正確;
④∵∠BAC+∠ABC=∠ACF,
∴$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC=$\frac{1}{2}$∠ACF,
∵∠BDC+∠DBC=$\frac{1}{2}$∠ACF,
∴$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ABC=∠BDC+∠DBC,
∵∠DBC=$\frac{1}{2}$∠ABC,
∴$\frac{1}{2}$∠BAC=∠BDC,即∠BDC=$\frac{1}{2}$∠BAC.
故④正確.
故選C.
點(diǎn)評(píng) 本題主要考查了三角形的內(nèi)角和,平行線的判定和性質(zhì),三角形外角的性質(zhì)等知識(shí),解題的關(guān)鍵是正確找各角的關(guān)系.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 星期天早晨,小明騎自行車從家里到植物園,途中到早餐店吃飯花了一段時(shí)間,然后繼續(xù)騎行,直至到達(dá)植物園(假設(shè)在騎自行車過(guò)程中勻速行駛).
星期天早晨,小明騎自行車從家里到植物園,途中到早餐店吃飯花了一段時(shí)間,然后繼續(xù)騎行,直至到達(dá)植物園(假設(shè)在騎自行車過(guò)程中勻速行駛).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖,小山崗的斜坡AC的坡度是tanα=$\frac{3}{4}$,在與山腳C距離200m的D處,測(cè)得山頂A的仰角為26.6°,則小山崗的高AB=300米(結(jié)果取整數(shù):參考數(shù)據(jù):sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).
如圖,小山崗的斜坡AC的坡度是tanα=$\frac{3}{4}$,在與山腳C距離200m的D處,測(cè)得山頂A的仰角為26.6°,則小山崗的高AB=300米(結(jié)果取整數(shù):參考數(shù)據(jù):sin26.6°=0.45,cos26.6°=0.89,tan26.6°=0.50).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
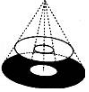 圓桌面(桌面中間有一個(gè)直徑為0.4m的圓洞)正上方的燈泡(看作一個(gè)點(diǎn))發(fā)出的光線照射平行于地面的桌面后,在地面上形成如圖所示的圓環(huán)形陰影.已知桌面直徑為1.2m,桌面離地面1m,若燈泡離地面3m,則地面圓環(huán)形陰影的面積是( )
圓桌面(桌面中間有一個(gè)直徑為0.4m的圓洞)正上方的燈泡(看作一個(gè)點(diǎn))發(fā)出的光線照射平行于地面的桌面后,在地面上形成如圖所示的圓環(huán)形陰影.已知桌面直徑為1.2m,桌面離地面1m,若燈泡離地面3m,則地面圓環(huán)形陰影的面積是( )| A. | 0.324π m2 | B. | 0.288π m2 | C. | 1.08π m2 | D. | 0.72π m2 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | b的指數(shù)是0 | B. | b沒(méi)有系數(shù) | C. | a是單項(xiàng)式 | D. | -3是一次單項(xiàng)式 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖,已知在△ABC中,∠B與∠C的平分線交于點(diǎn)P,∠BPC=125°時(shí),則∠A=70°.
如圖,已知在△ABC中,∠B與∠C的平分線交于點(diǎn)P,∠BPC=125°時(shí),則∠A=70°.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:選擇題
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com