
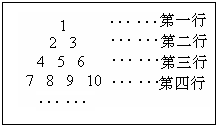
 如圖所示,是一個自然數排列的三角形數陣:根據該數陣的規律,第6行第3個數是18,第20行第2個數是192.
如圖所示,是一個自然數排列的三角形數陣:根據該數陣的規律,第6行第3個數是18,第20行第2個數是192. 分析 觀察數據得到第一行有1個數,第二行有2個數,…,即每行的數字的個數等于此行的行數,則第五行最后一個數為1+2+3+4+5=15,再加數三個數得到第6行第3個數;
由于第(n-1)行有(n-1)個數,則第n-1行最后一個數為1+2+3+4+5+…+n-1=$\frac{n(n-1)}{2}$,然后再加兩個數即可得到第n行第2個數.
解答 解:第一行有1個數,
第二行有2個數,
第三行有3個數,
第四行有4個數,
第五行有5個數,則第五行最后一個數為1+2+3+4+5=15,
所以第六行有6個數,其中第一個數為16,第二個數為17,第三個數為18,
…
第(n-1)行有(n-1)個數,則第n-1行最后一個數為1+2+3+4+5+…+n-1=$\frac{n(n-1)}{2}$,
所以第n行第一個數為$\frac{n(n-1)}{2}$+1,第二個數為$\frac{n(n-1)}{2}$+2.
當n=20時,$\frac{n(n-1)}{2}$+2=192
故答案為18,192.
點評 本題考查了規律型:數字的變化類:通過從一些特殊的數字變化中發現不變的因素或按規律變化的因素,然后推廣到一般情況.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:選擇題

| A. | 球體 | B. | 圓柱 | C. | 圓錐 | D. | 球體或圓錐 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
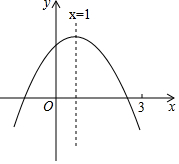 二次函數y=ax2+bx+c(a≠0)圖象如圖,下列結論正確的是( )
二次函數y=ax2+bx+c(a≠0)圖象如圖,下列結論正確的是( )| A. | abc>0 | |
| B. | 若ax12+bx1=ax22+bx2且x1≠x2,則x1+x2=1 | |
| C. | a-b+c>0 | |
| D. | 當m≠1時,a+b>am2+bm |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
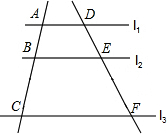 如圖,l1∥l2∥l3,直線a,b與l1,l2,l3分別相交于A,B,C和點D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,則EF的長是( )
如圖,l1∥l2∥l3,直線a,b與l1,l2,l3分別相交于A,B,C和點D,E,F,若$\frac{AB}{BC}$=$\frac{3}{5}$,DE=6,則EF的長是( )| A. | $\frac{18}{5}$ | B. | $\frac{48}{5}$ | C. | 10 | D. | 6 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
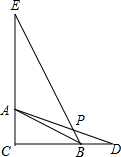 已知,Rt△ABC中∠C=90°,點D在邊CB的延長線上,BD=AC,點E在邊CA的延長線上,AE=CD,連接BE、AD交于點P,若BC=2BD=2,則PE=$\frac{{9\sqrt{5}}}{5}$.
已知,Rt△ABC中∠C=90°,點D在邊CB的延長線上,BD=AC,點E在邊CA的延長線上,AE=CD,連接BE、AD交于點P,若BC=2BD=2,則PE=$\frac{{9\sqrt{5}}}{5}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com