Question

如圖，反比例函數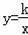（k＞0）與長方形OABC在第一象限相交于D、E兩點，OA=2，OC=4，連接OD、OE、DE．記△OAD、△OCE的面積分別為S₁、S₂．

（1）①點B坐標為　　　　　　；②S₁　　　　　　S₂（填“＞”、“＜”、“=”）；

（2）當點D為線段AB的中點時，求k的值及點E坐標；

（3）當S₁+S₂=2時，試判斷△ODE的形狀，并求△ODE的面積．

Answer 1

【考點】反比例函數綜合題．

【分析】（1）根據OA=2，OC=4可直接得到點B坐標；②根據反比例函k的意義可知S₁、S₂都等于|k|，即可得到答案；

（2）當點D為AB中點時，AD=2，得出D的坐標是（2，2），求出解析式即可；

（3）根據當S₁+S₂=2時，由（1）得出S₁=S₂=1，進而得出BD，BE的長，進而得出DO²+DE²=OE²，△ODE是直角三角形，進而得出三角形面積．

【解答】解：（1）①根據長方形OABC中，OA=2，OC=4，

則點B坐標為（4，2），

②∵反比例函數（k＞0）與長方形OABC在第一象限相交于D、E兩點，

利用△OAD、△OCE的面積分別為S₁=AD•AO，S₂=•CO•EC，xy=k，得出，

S₁=AD•AO=k，S₂=•CO•EC=k，

∴S₁=S₂；

（2）當點D為AB中點時，AD=2，

∴D的坐標是（2，2），

把D（2，2）代入y=得：

k=2×2=4，

∴y=．

∵點B坐標為（4，2），

∴E點橫坐標為：4，

∴4×y=4，

∴y=1，

∴E點坐標為：（4，1）；

（3）當S₁+S₂=2時，∵S₁=S₂，

∴S₁=S₂=1，

∵S₁=AD•AO=AD×2=1，

∴AD=1，

∵S₂=•CO•EC=×4×EC=1，

∴EC=，

∵OA=2，OC=4，

∴BD=4﹣1=3，

BE=2﹣=，

∴DO²=AO²+AD²=4+1=5，

DE²=DB²+BE²=9+=，

OE²=CO²+CE²=16+=，

∴DO²+DE²=OE²，

∴△ODE是直角三角形，

∵DO²=5，

∴DO=，

∵DE²=，

∴DE=，

∴△ODE的面積為：×DO×DE=××=．