
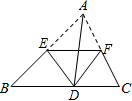
 在三角形紙片ABC中.點E為AB邊中點,將△ABC沿過點E的直線折疊,折痕交AC于F,并使點A與落在BC邊上的點D.求證:點F平分AC.
在三角形紙片ABC中.點E為AB邊中點,將△ABC沿過點E的直線折疊,折痕交AC于F,并使點A與落在BC邊上的點D.求證:點F平分AC. 分析 根據折疊的性質得到DA=DF,AE=FE,∠ADE=∠FDE,根據等腰三角形性質得∠B=∠DFB,再根據三角形外角性質得到∠ADE+∠FDE=∠B+∠DFB,則∠ADE=∠B,所以DE∥BC,易得DE為△ABC的中位線,得到AE=EC,于是EF=EC.
解答 證明:∵將△ABC沿過點E的直線折疊,折痕交AC于F,并使點A與落在BC邊上的點D,
∴DA=DF,AE=FE,∠ADE=∠FDE,
∴∠B=∠DFB,
∵∠ADF=∠B+∠DFB,即∠ADE+∠FDE=∠B+∠DFB,
∴∠ADE=∠B,
∴DE∥BC,
∵D為AB的中點,
∴DE為△ABC的中位線,
∴AE=EC,
∴EF=EC,
即點F平分AC.
點評 本題考查了折疊的性質:折疊是一種對稱變換,它屬于軸對稱,折疊前后圖形的形狀和大小不變,位置變化,對應邊和對應角相等.也考查了三角形中位線性質.


科目:初中數學 來源: 題型:選擇題
| A. | 368×103cm | B. | 36.8×104cm | C. | 3.68×105cm | D. | 3.68×106cm |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 100cm | B. | 10cm | C. | 10cm或2$\sqrt{7}$cm | D. | 100cm或28cm |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com