【題目】已知二次函數
（
為常數）．
（1）求證：不論為何值，該函數的圖像與
軸總有公共點；
（2）當取什么值時，該函數的圖像與
軸的交點在軸的下方？
【答案】（1）見解析；（2）當
時，
，即該函數的圖像與
軸交點的縱坐標是
；（3）當
，即
時，該函數的圖像與軸的交點在
軸的下方
【解析】
（1）方法一令
,求解方程的根即可,方法二根據根的判別式判斷,（2）根據軸的下方的點的縱坐標為負,列不等式即可解題.
（1）證明：
方法一：當時，
．
解得
，
．
當
，即
時，方程有兩個相等的實數根；當
，即
時，方程有兩個不相等的實數根．
所以，不論
為何值，該函數的圖像與軸總有公共點．
方法二：將原表達式化為
．
因為一元二次方程
的根的判別式
．
所以，不論為何值，該函數的圖像與軸總有公共點．
（2）解：當時，，即該函數的圖像與軸交點的縱坐標是．
∴當，即
時，該函數的圖像與軸的交點在軸的下方．
科目：初中數學 來源： 題型：
【題目】如圖，在一個可以自由轉動的轉盤中，指針位置固定，三個扇形的面積都相等，且分別標有數字1，2，3．
（1）小明轉動轉盤一次，當轉盤停止轉動時，指針所指扇形中的數字是奇數的概率為________；
（2）小明先轉動轉盤一次，當轉盤停止轉動時，記錄下指針所指扇形中的數字；接著再轉動轉盤一次，當轉盤停止轉動時，再次記錄下指針所指扇形中的數字，求這兩個數字之和是3的倍數的概率(用畫樹狀圖或列表等方法求解)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在北海市創建全國文明城活動中，需要30名志愿者擔任“講文明樹新風”公益廣告宣傳工作，其中男生18人，女生12人．
（1）若從這30人中隨機選取一人作為“展板掛圖”講解員，求選到女生的概率；
（2）若“廣告策劃”只在甲、乙兩人中選一人，他們準備以游戲的方式決定由誰擔任，游戲規則如下：將四張牌面數字分別為2，3，4，5的撲克牌洗勻后，數字朝下放于桌面，從中任取2張，若牌面數字之和為偶數，則甲擔任，否則乙擔任．試問這個游戲公平嗎？請用樹狀圖或列表法說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，∠AOB=90°，且OA、OB分別與反比例函數y=
（x＞0）、y=﹣
（x＜0）的圖象交于A、B兩點，則tan∠OAB的值是（ ）
A. 
B. 
C. 1 D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
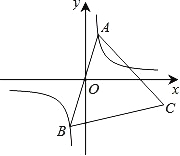
【題目】如圖，已知點A是雙曲線
在第一象限分支上的一個動點，連結AO并延長交另一分支于點B，以AB為邊作等邊三角形ABC，點C在第四象限內，且隨著點A的運動，點C的位置也在不斷變化，但點C始終在雙曲線
上運動，則k的值是 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，一次函數
的圖象與y軸交于點A，
與x軸交于點B，與反比例函數
的圖象分別交于點M，N，已知△AOB的面積為1，點M的縱坐
標為2，
（1）求一次函數和反比例函數的解析式；
（2）直接寫出
時x的取值范圍．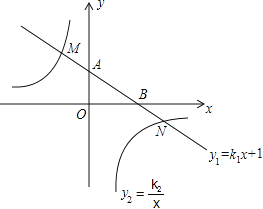
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC中，AB = AC，點D是邊BC的中點，過點A、D分別作BC與AB的平行線，相交于點E，連結EC、AD.
求證：四邊形ADCE是矩形.
查看答案和解析>>
科目：初中數學 來源： 題型：
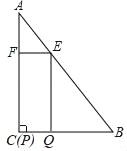
【題目】如圖，在△ABC中，∠A＝30°，∠C＝90°，AB＝12，四邊形EFPQ是矩形，點P與點C重合，點Q、E、F分別在BC、AB、AC上（點E與點A、點B均不重合）．
（1）當AE＝8時，求EF的長；
（2）設AE＝x，矩形EFPQ的面積為y．
①求y與x的函數關系式；
②當x為何值時，y有最大值，最大值是多少？
（3）當矩形EFPQ的面積最大時，將矩形EFPQ以每秒1個單位的速度沿射線CB勻速向右運動（當點P到達點B時停止運動），設運動時間為t秒，矩形EFPQ與△ABC重疊部分的面積為S，求S與t的函數關系式，并寫出t的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
