
如圖,▱ABCD中,∠ABC=60°,E、F分別在CD和BC的延長線上,AE∥BD,EF⊥BC,EF=
 ,則AB的長是 .
,則AB的長是 .


1 .
【考點】平行四邊形的判定與性質;含30度角的直角三角形;勾股定理.
【分析】根據平行四邊形性質推出AB=CD,AB∥CD,得出平行四邊形ABDE,推出DE=DC=AB,根據直角三角形性質求出CE長,即可求出AB的長.
【解答】解:∵四邊形ABCD是平行四邊形,
∴AB∥DC,AB=CD,
∵AE∥BD,
∴四邊形ABDE是平行四邊形,
∴AB=DE=CD,
即D為CE中點,
∵EF⊥BC,
∴∠EFC=90°,
∵AB∥CD,
∴∠DCF=∠ABC=60°,
∴∠CEF=30°,
∵EF=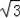
 ,
,
∴CE=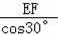
 =2,
=2,
∴AB=1,
故答案為:1.
【點評】本題考查了平行四邊形的性質和判定,平行線性質,勾股定理,直角三角形斜邊上中線性質,含30度角的直角三角形性質等知識點的應用,此題綜合性比較強,是一道比較好的題目.


 海淀黃岡名師導航系列答案
海淀黃岡名師導航系列答案 普通高中同步練習冊系列答案
普通高中同步練習冊系列答案科目:初中數學 來源: 題型:
已知關于x的一元二次方程(a﹣1)x2﹣2x+1=0有兩個不相等的實數根,則a的取值范圍是( )
A.a>2 B.a<2 C.a<2且a≠l D.a<﹣2
查看答案和解析>>
科目:初中數學 來源: 題型:
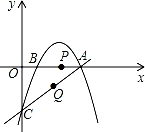
已知直線y=kx﹣3與x軸交于點A (4,0),與y軸交于點C.拋物線y=﹣
(4,0),與y軸交于點C.拋物線y=﹣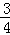 x2+mx+n經過點A和點C.且與x軸交于點B,動點P在x軸上以每秒1個單位長度的速度由點B向點A運動.點Q由點C沿線段CA向點A運動.且速度是點P運動速度的2倍.
x2+mx+n經過點A和點C.且與x軸交于點B,動點P在x軸上以每秒1個單位長度的速度由點B向點A運動.點Q由點C沿線段CA向點A運動.且速度是點P運動速度的2倍.
(1)求直線的解析式和拋物線的解析式;
(2)如果點P和點Q同時出發.運動時間為t(秒).試問當t為何值時,以A、P、Q為頂點的三角形與△AOC相 似.
似.
查看答案和解析>>
科目:初中數學 來源: 題型:
種植能手李大叔種植了一批新品種黃瓜,為了考察這種黃瓜的生長情況,李大叔抽查了部分黃瓜株上長出的黃瓜根數,得到如圖的條形圖,則抽查的這部分黃瓜株上所結黃瓜根數的中位數和眾數分別是( )
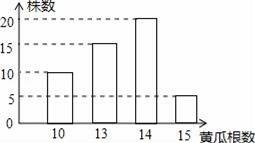

A.13.5,20 B.15,5 C.13.5,14 D.13,14
查看答案和解析>>
科目:初中數學 來源: 題型:
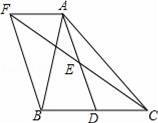
如圖,在△ABC中,D是BC邊上的一點,E是AD的中點,過A點作BC的平行線交CE的延長線于點F,且AF=BD,連接BF.
(1)BD與CD有什么數量關系,并說明理由;
(2)當△ABC滿足什么條件時,四邊形AFBD是矩形?并說明理由.
(3)在(2)的條件下,△ABC滿足條件 ,矩形AFBD是正方形.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com