
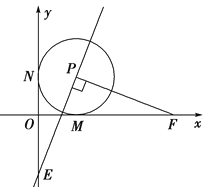
【題目】已知O是坐標原點,以P(1,1)為圓心的⊙P與x軸、y軸分別相切于點M和點N.點F從點M出發,沿x軸正方向以每秒1個單位長度的速度運動,連結PF,過點P作PE⊥PF交y軸于點E.設點F運動的時間是t秒(t>0).
(1)求點E的坐標(用t表示);
(2)在點F運動過程中,當PF=2OE時,求t的值.
(3)當t>1時,作點F關于點M的對稱點F′.點Q是線段MF′的中點,連結QE.在點F運動過程中,是否存在某一時刻,使得△QOE與△PMF相似,若存在,求出t的值;若不存在,請說明理由.
【答案】(1)E(0,1-t);(2)![]() 或
或![]() ;(3)存在:當t=
;(3)存在:當t=![]() ,t=
,t=![]() ,t=2+
,t=2+![]() 時,使得△QOE與△PMF相似.
時,使得△QOE與△PMF相似.
【解析】試題分析:
(1)連接PM、PN,由已知條件易證△PMF≌△PNE,由此可得NE=MF=t,則可得OE=t-1,結合點E在y軸的負半軸即可得到點E的坐標了;
(2)在Rt△PFM中,易得PF=![]() ,結合OE=
,結合OE=![]() 即可得到方程
即可得到方程![]() ,解此方程即可求得對應的t的值;
,解此方程即可求得對應的t的值;
(3)由F(1+t,0),F和F′關于點M對稱可得F′(1-t,0),結合點Q是線段MF′的中點可得Q(1-![]() t,0),然后在1<t<2時,分△OEQ∽△MPF和△OEQ∽△MFP兩種情況討論計算可求得對應的t的值;在當t>2時,分△OEQ ∽△MPF和△OEQ ∽△MFP兩種情況討論計算可求得對應的t的值.
t,0),然后在1<t<2時,分△OEQ∽△MPF和△OEQ∽△MFP兩種情況討論計算可求得對應的t的值;在當t>2時,分△OEQ ∽△MPF和△OEQ ∽△MFP兩種情況討論計算可求得對應的t的值.
試題解析:
(1)如下圖,連結PM,PN.
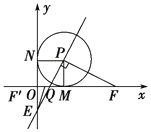
∵以P(1,1)為圓心的⊙P與x軸、y軸分別相切于點M和點N,
∴∠PNE=∠PMF=∠MPN=90°,
∴∠NPE+∠EPM=∠EPM+∠MPF=90°,
∴∠NPE=∠MPF,
又∵PM=PN,
∴△PMF≌△PNE,
∴NE=MF=t,
∴OE=t-1,
∴E(0,1-t);
(2)在直角△PMF中![]() ,
, ![]() ,
,
由PF=2OE得![]()
![]() ,
,
解得![]() 或
或![]() .
.
(3)存在,理由如下;
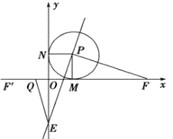
∵F(1+t,0),F和F′關于點M對稱,
∴F′(1-t,0),
∵點Q是MF′的中點,
∴Q(1-![]() t,0),
t,0),
①當1<t<2時,如圖,有OQ=1-![]() t,
t,
由(1)得∴NE=MF=t,OE=t-1.
當△OEQ∽△MPF時,
∴![]() ,
,
∴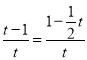 ,
,
解得,t=![]() 或t=
或t=![]() (舍去);
(舍去);
當△OEQ∽△MFP時, ![]() ,
,
∴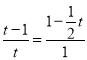 ,解得,t=
,解得,t=![]() 或t=
或t=![]() (舍去);
(舍去);
②當t>2時,如圖,有OQ=![]() t-1,
t-1,
由(1)得NE=MF=t,OE=t-1,
當△OEQ ∽△MPF, ![]() ,
,
∴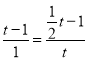 ,無解;
,無解;
當△OEQ ∽△MFP時, ![]() ;
;
∴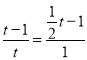 ,
,
解得![]() 或
或![]() (舍去).
(舍去).
綜上所述,當t=![]() ,t=
,t=![]() ,
, ![]() 時,使得△QOE與△PMF相似.
時,使得△QOE與△PMF相似.


科目:初中數學 來源: 題型:
【題目】典典同學學完統計知識后,隨機調查了她家所在轄區若干名居民的年齡,將調查數據繪制成如下扇形和條形統計圖:
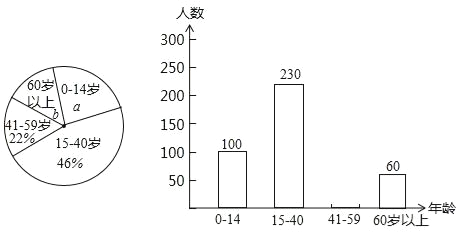
請根據以上不完整的統計圖提供的信息,解答下列問題:
(1)扇形統計圖中a= ,b= ;并補全條形統計圖;
(2)若該轄區共有居民3500人,請估計年齡在0~14歲的居民的人數.
(3)一天,典典知道了轄區內60歲以上的部分老人參加了市級門球比賽,比賽的老人們分成甲、乙兩組,典典很想知道甲乙兩組的比賽結果,王大爺告訴說,甲組與乙組的得分和為110,甲組得分不低于乙組得分的1.5倍,甲組得分最少為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:在三角形中,把一邊的中點到這條邊的高線的距離叫做這條邊的中垂距.
例:如圖①,在△ABC中,D為邊BC的中點,AE⊥BC于E,則線段DE的長叫做邊BC的中垂距.
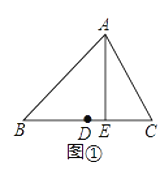
(1)設三角形一邊的中垂距為d(d≥0).若d=0,則這樣的三角形一定是________,推斷的數學依據是________.
(2)如圖②,在△ABC中,∠B=45°,AB=![]() ,BC=8,AD為邊BC的中線,求邊BC的中垂距.
,BC=8,AD為邊BC的中線,求邊BC的中垂距.

(3)如圖③,在矩形ABCD中,AB=6,AD=4.點E為邊CD的中點,連結AE并延長交BC的延長線于點F,連結AC.求△ACF中邊AF的中垂距.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為紀念李時珍誕辰500周年,蘄春縣投巨資建設如圖所示展覽館,其外框是一個大正方形,中間四個大小相同的正方形(陰影部分)是支展館的核心筒,標記了字母的五個大小相同的正方形是展廳,剩余的四個大小相同的圖形是休息廳,已知核心筒的正方形邊長比展廳的正方形邊長的一半多1米
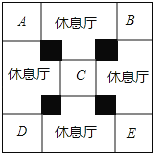
(1)若設展廳的正方形邊長為a米,則用含a的代數式表示核心筒的正方形邊長為 米.
(2)若設核心筒的正方形邊長為b米,求該展館外框大正方形的周長(用含b的代數式表示).
(3)若展覽館外框大正形邊長為26米,求休息廳的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, ![]() 是
是 ![]() 內一點,
內一點, ![]() 與
與 ![]() 相交于
相交于 ![]() 、
、![]() 兩點,且與
兩點,且與 ![]() 、
、![]() 分別相切于點
分別相切于點 ![]() 、
、![]() ,
, ![]() .連接
.連接 ![]() 、
、![]() .
.
(1)求證: ![]() .
.
(2)已知 ![]() ,
, ![]() .求四邊形
.求四邊形 ![]() 是矩形時
是矩形時 ![]() 的半徑.
的半徑.
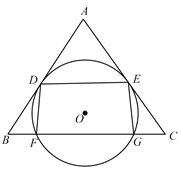
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數![]() 的圖象與y軸正半軸相交,其頂點坐標為(
的圖象與y軸正半軸相交,其頂點坐標為(![]() ,1),下列結論:①abc>0;②a=b;③a=4c﹣4;④方程
,1),下列結論:①abc>0;②a=b;③a=4c﹣4;④方程![]() 有兩個相等的實數根,其中正確的結論是______.(只填序號即可).
有兩個相等的實數根,其中正確的結論是______.(只填序號即可).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】輪船沿江從A港順流行駛到B港,比從B港返回A港少用3小時,若船速為26千米/時,水速為2千米/時,求A港和B港相距多少千米.設A港和B港相距x千米.根據題意,可列出的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知矩形ABCD中,E是AD邊上的一個動點,點F,G,H分別是BC,BE,CE的中點.
(1)求證:△BGF≌△FHC;
(2)設AD=a,當四邊形EGFH是正方形時,求矩形ABCD的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸上點A,B,C的位置如圖,點C是線段AB的中點,點A表示的數比點C表示的數的兩倍還大3,點B和點C表示的數是互為相反數,點C表示的數是__________.
![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com