
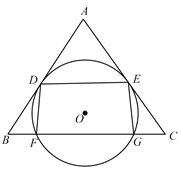
【題目】如圖, ![]() 是
是 ![]() 內一點,
內一點, ![]() 與
與 ![]() 相交于
相交于 ![]() 、
、![]() 兩點,且與
兩點,且與 ![]() 、
、![]() 分別相切于點
分別相切于點 ![]() 、
、![]() ,
, ![]() .連接
.連接 ![]() 、
、![]() .
.
(1)求證: ![]() .
.
(2)已知 ![]() ,
, ![]() .求四邊形
.求四邊形 ![]() 是矩形時
是矩形時 ![]() 的半徑.
的半徑.
【答案】(1)見解析;(2)![]()
【解析】試題分析:
(1)由AB、AC和⊙O相切于點D、E可得AD=AE,由此可得∠ADE=∠AED,結合DE∥BC,可得∠B=∠C,即可得到AB=AC了;
(2)如下圖,連接AO交DE于點M,延長AO交BC于點N,連接OD、OE和DG,設⊙O的半徑為r,由已知條件易證BN=3,∠ANB=90°,從而可得AN=4,在證△ADO∽△ANB,由此可得![]() ,即
,即![]() 從而可得AD=
從而可得AD= ![]() ,則BD=
,則BD= ![]() ,再證△BDG∽△BNA可得
,再證△BDG∽△BNA可得![]() ,即
,即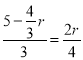 ,由此即可解得:
,由此即可解得: ![]() .
.
試題解析:
(1)∵![]() 與
與 ![]() 、
、![]() 分別相切于點
分別相切于點 ![]() 、
、![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
, ![]() .
.
∴![]() .
.
∴![]() ;
;
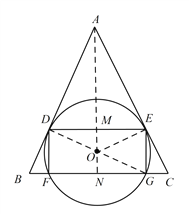
(2) 如圖,連接 ![]() ,交
,交 于點
![]() ,延長
,延長 ![]() 交
交 ![]() 于點
于點 ![]() ,連接OD、
,連接OD、 ![]() 、
、![]() ,設
,設 ![]() 的半徑為
的半徑為 ![]() ,
,
∵ 四邊形 ![]() 是矩形,
是矩形,
∴∠DEG=90°,
∴![]() 是
是 ![]() 的直徑.
的直徑.
∵![]() ,AN平分∠BAC,
,AN平分∠BAC,
∴![]() ∠ANB=90°,
∠ANB=90°,
∴在Rt△ABN中可得:AN=4,
∵AB和⊙O相切于點D,
∴∠ADO=∠GDB=90°=∠ANB,
∵∠DAO=∠NAB,
∴△ADO∽△ANB,
∴![]() ,即
,即![]() ,
,
∴AD= ![]() ,
,
∵∠GDB=∠ANB=90°,∠B=∠B,
∴△BDG∽△BNA,
∴![]() ,即
,即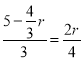 ,解得:
,解得: ![]() .
.
∴四邊形 ![]() 是矩形時
是矩形時 ![]() 的半徑為
的半徑為 ![]() .
.


科目:初中數學 來源: 題型:
【題目】華聯超市第一次用7000元購進甲、乙兩種商品,其中甲商品的件數是乙商品件數的2倍,甲、乙兩種商品的進價和售價如表:(注:獲利=售價﹣進價)
甲 | 乙 | |
進價(元/件) | 20 | 30 |
售價(元/件) | 25 | 40 |
(1)該超市購進甲、乙兩種商品各多少件?
(2)該超市將第一次購進的甲、乙兩種商品全部賣完后一共可獲得多少利潤?
(3)該超市第二次以第一次的進價又購進甲、乙兩種商品,其中甲商品的件數不變,乙商品的件數是第一次的3倍:甲商品按原價銷售,乙商品打折銷售,第二次兩種商品都售完以后獲得的總利潤比第一次獲得的總利潤多800元,求第二次乙商品是按原價打幾折銷售?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為增強學生體質,各學校普遍開展了陽光體育活動,某校為了解全校1000名學生每周課外體育活動時間的情況,隨機調查了其中的50名學生,對這50名學生每周課外體育活動時間x(單位:小時)進行了統計.根據所得數據繪制了一幅不完整的統計圖,并知道每周課外體育活動時間在6≤x<8小時的學生人數占24%.根據以上信息及統計圖解答下列問題:
(1)本次調查屬于 調查,樣本容量是 ;
(2)請補全頻數分布直方圖中空缺的部分;
(3)求這50名學生每周課外體育活動時間的平均數;
(4)估計全校學生每周課外體育活動時間不少于6小時的人數.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某一城市美化工程招標時,有甲、乙兩個工程隊投標.經測算:甲隊單獨完成這項工程需要60天,乙隊單獨完成這項工程需要90天;若由甲隊先做20天,剩下的工程由甲、乙兩隊合做完成.
(1)甲、乙兩隊合作多少天?
(2)甲隊施工一天需付工程款3.5萬元,乙隊施工一天需付工程款2萬元.若該工程計劃在70天內完成,在不超過計劃天數的前提下,是由甲隊或乙隊單獨完成該工程省錢?還是由甲乙兩隊全程合作完成該工程省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一般情況下![]() +
+![]() =
=![]() 不成立,但有些數可以使得它成立,例如:a=b=0.我們稱使得
不成立,但有些數可以使得它成立,例如:a=b=0.我們稱使得![]() +
+![]() =
=![]() 成立的一對數a,b為“相伴數對”,記為(a,b).
成立的一對數a,b為“相伴數對”,記為(a,b).
(1)若(1,b)是“相伴數對”,求b的值;
(2)寫出一個“相伴數對”(a,b),其中a,b為整數且a≠0;
(3)若(m,n)是“相伴數對”,求代數式m﹣![]() n﹣[4m﹣2(3n﹣1)]的值.
n﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
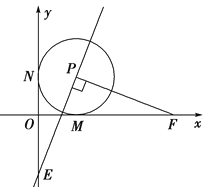
【題目】已知O是坐標原點,以P(1,1)為圓心的⊙P與x軸、y軸分別相切于點M和點N.點F從點M出發,沿x軸正方向以每秒1個單位長度的速度運動,連結PF,過點P作PE⊥PF交y軸于點E.設點F運動的時間是t秒(t>0).
(1)求點E的坐標(用t表示);
(2)在點F運動過程中,當PF=2OE時,求t的值.
(3)當t>1時,作點F關于點M的對稱點F′.點Q是線段MF′的中點,連結QE.在點F運動過程中,是否存在某一時刻,使得△QOE與△PMF相似,若存在,求出t的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】風電已成為我國繼煤電、水電之后的第三大電源,風電機組主要由塔桿和葉片組成(如圖1),圖2是從圖1引出的平面圖.假設你站在A處測得塔桿頂端C的仰角是55°,沿HA方向水平前進43米到達山底G處,在山頂B處發現正好一葉片到達最高位置,此時測得葉片的頂端D(D、C、H在同一直線上)的仰角是45°.已知葉片的長度為35米(塔桿與葉片連接處的長度忽略不計),山高BG為10米,BG⊥HG,CH⊥AH,求塔桿CH的高.(參考數據:tan55°≈1.4,tan35°≈0.7,sin55°≈0.8,sin35°≈0.6)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com