
【題目】“低碳生活,綠色出行”是我們倡導的一種生活方式,有關部門抽樣調查了某單位員工上下班的交通方式,繪制了如下統計圖:
(1)樣本中的總人數為 ,開私家車的人數![]() ,扇形統計圖中“騎自行車”所在扇形的圓心角為 度;(直接寫出答案)
,扇形統計圖中“騎自行車”所在扇形的圓心角為 度;(直接寫出答案)
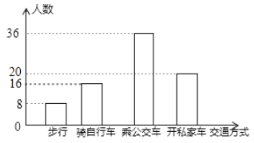
(2)補全條形統計圖;
(3)該單位共有500人,積極踐行這種生活方式,越來越多的人上下班由開私家車改為騎自行車.若步行、坐公交車上下班的人數保持不變,問原來開私家車的人中至少有多少人改為騎自行車,才能使騎自行車的人數不低于開私家車的人數?
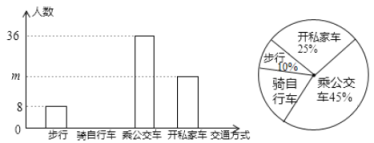
【答案】(1)160人;40;72;(2)詳見解析;(3)原來開私家車的人中至少有13人改為騎自行車,才能使騎自行車的人數不低于開私家車的人數.
【解析】
(1)由步行人數及其所占百分比可得總人數,總人數乘以私家車對應的百分比可得其人數,用360°乘以自行車對應的百分比可得答案;
(2)用總人數乘以騎自行車對應的百分比可得其人數,據此可補全條形圖;
(3)設原來開私家車的人中有x人改為騎自行車,表示出改后騎自行車的人數和開私家車的人數,列式不等式,求解即可.
解:(1)樣本中的總人數為16÷10%=160(人),
開私家車的人數m=160×25%=40(人),
扇形統計圖中“騎自行車”所在扇形的圓心角為360°×20%=72°,
故答案為:160人;40;72;
(2)騎自行車的人數為160×20%=32(人),
補全條形圖如下:
(3)設原來開私家車的人中有![]() 人改為騎自行車,得
人改為騎自行車,得
![]()
解得,![]() .
.
答:原來開私家車的人中至少有13人改為騎自行車,才能使騎自行車的人數不低于開私家車的人數.


科目:初中數學 來源: 題型:
【題目】某校為檢測“停課不停學”期間九年級學生的復習情況,進行了中考數學模擬測試并從中隨機抽取了部分學生的測試成績分成![]() 個小組,根據每個小組的人數繪制如圖所示的尚不完整的頻數分布直方圖.
個小組,根據每個小組的人數繪制如圖所示的尚不完整的頻數分布直方圖.
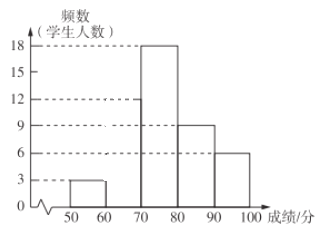
請根據信息回答下列問題:
![]() 若成績在
若成績在![]() 分的頻率為
分的頻率為![]() ,請計算抽取的學生人數并補全頻數分布直方圖;
,請計算抽取的學生人數并補全頻數分布直方圖;
![]() 在此次測試中,抽取學生成績的中位數在______ 分數段中;
在此次測試中,抽取學生成績的中位數在______ 分數段中;
![]() 若該校九年級共有
若該校九年級共有![]() 名學生,成績在
名學生,成績在![]() 分以上的(含
分以上的(含![]() 分)為優秀,請通過計算說明,大約有多少名學生在本次測試中數學成績為優秀.
分)為優秀,請通過計算說明,大約有多少名學生在本次測試中數學成績為優秀.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的小正方形組成的網格中,四邊形ABCD的四個頂點都在格點上,請按要求完成下列各題.
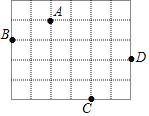
(1)線段AB的長為__,BC的長為__,CD的長為__,AD的長為__;
(2)連接AC,通過計算△ACD的形狀是__;△ABC的形狀是__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 與
與![]() 軸交于點A和點B(3,0),與
軸交于點A和點B(3,0),與![]() 軸交于點C(0,3).
軸交于點C(0,3).

(1)求拋物線的解析式;
(2)若點M是拋物線在![]() 軸下方上的動點,過點M作MN//
軸下方上的動點,過點M作MN//![]() 軸交直線BC于點N,求線段MN的最大值;
軸交直線BC于點N,求線段MN的最大值;
(3)在(2)的條件下,當MN取最大值時,在拋物線的對稱軸![]() 上是否存在點P,使△PBN是等腰三角形?若存在,請直接寫出所有點P的坐標;若不存在,請說明理由.
上是否存在點P,使△PBN是等腰三角形?若存在,請直接寫出所有點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 、
、![]() 分別在邊
分別在邊![]() 、
、![]() 上,
上,![]() ,連結
,連結![]() ,點
,點![]() 、
、![]() 、
、![]() 分別為
分別為![]() 、
、![]() 、
、![]() 的中點.
的中點.
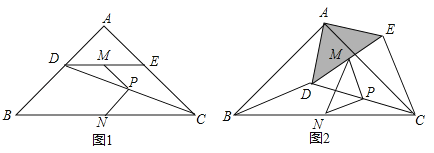
(1)觀察猜想圖1中,線段![]() 與
與![]() 的數量關系是_______,位置關系是_______;
的數量關系是_______,位置關系是_______;
(2)探究證明把![]() 繞點
繞點![]() 逆時針方向旋轉到圖2的位置,連結
逆時針方向旋轉到圖2的位置,連結![]() 、
、![]() 、
、![]() ,判斷
,判斷![]() 的形狀,并說明理由;
的形狀,并說明理由;
(3)拓展延伸把![]() 繞點
繞點![]() 在平面內自由旋轉,若
在平面內自由旋轉,若![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在反比例函數y= ![]() 的圖象上有一動點A,連接AO并延長交圖象的另一支于點B,在第二象限內有一點C,滿足AC=BC,當點A運動時,點C始終在函數y=
的圖象上有一動點A,連接AO并延長交圖象的另一支于點B,在第二象限內有一點C,滿足AC=BC,當點A運動時,點C始終在函數y= ![]() 的圖象上運動,若tan∠CAB=2,則k的值為( )
的圖象上運動,若tan∠CAB=2,則k的值為( )
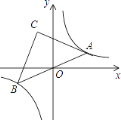
A. ﹣3 B. ﹣6 C. ﹣9 D. ﹣12
查看答案和解析>>
科目:初中數學 來源: 題型:
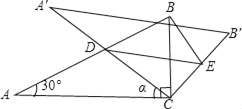
【題目】如圖,將含30°角的直角三角板ABC(∠A=30°)繞其直角頂點C順時針旋轉α角(0°<α<90°),得到Rt△A′B′C,A′C與AB交于點D,過點D作DE∥A′B′交CB′于點E,連接BE.易知,在旋轉過程中,△BDE為直角三角形.設BC=1,AD=x,△BDE的面積為S.
(1)當α=30°時,求x的值.
(2)求S與x的函數關系式,并寫出x的取值范圍;
(3)以點E為圓心,BE為半徑作⊙E,當S=![]() 時,判斷⊙E與A′C的位置關系,并求相應的tanα值.
時,判斷⊙E與A′C的位置關系,并求相應的tanα值.
查看答案和解析>>
科目:初中數學 來源: 題型:
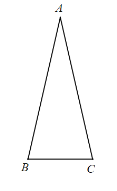
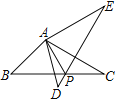
【題目】如圖,△ABC 中,AB=AC, ∠BAC <60°,將線段 AB 繞點 A逆時針旋轉 60°得到點 D, 點 E 與點 D 關于直線 BC 對稱,連接 CD,CE,DE.
(1)依題意補全圖形;
(2)判斷△CDE 的形狀,并證明;
(3)請問在直線CE上是否存在點 P,使得 PA - PB =CD 成立?若存在,請用文字描述出點 P 的準確位置,并畫圖證明;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題背景:如圖,將![]() 繞點
繞點![]() 逆時針旋轉60°得到
逆時針旋轉60°得到![]() ,
,![]() 與
與![]() 交于點
交于點![]() ,可推出結論:
,可推出結論:![]()
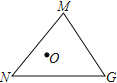
問題解決:如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() .點
.點![]() 是
是![]() 內一點,則點
內一點,則點![]() 到
到![]() 三個頂點的距離和的最小值是___________
三個頂點的距離和的最小值是___________
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com