能力評價系列答案
唐印文化課時測評系列答案科目：初中數學 來源： 題型：
以下是小辰同學閱讀的一份材料和思考：
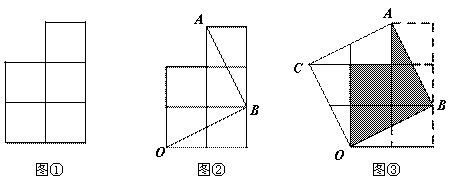五個邊長為1的小正方形如圖①放置，用兩條線段把它們分割成三部分(如圖②)，移動其中的兩部分，與未移動的部分恰好拼接成一個無空隙無重疊的新正方形(如圖③).
小辰閱讀后發現，拼接前后圖形的面積相等，若設新的正方形的邊長為x（x＞0），可得x2=5，x=
.由此可知新正方形邊長等于兩個小正方形組成的矩形的對角線長.
參考上面的材料和小辰的思考方法，解決問題：
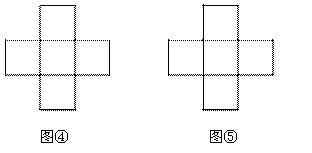
五個邊長為1的小正方形（如圖④放置），用兩條線段把它們分割成四部分，移動其中的兩部分，與未移動
的部分恰好拼接成一個無空隙無重疊的矩形，且所得矩形的鄰邊之比為1：2．
具體要求如下：
（1）設拼接后的長方形的長為a，寬為b，則a的長度為 ；
（2）在圖④中，畫出符合題意的兩條分割線（只要畫出一種即可）；
（3）在圖⑤中，畫出拼接后符合題意的長方形（只要畫出一種即可）
 |
查看答案和解析>>
科目：初中數學 來源： 題型：
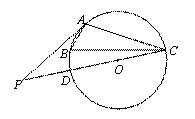
如圖，已知A、B、C分別是⊙O上的點，∠B=60°，P是直徑CD的延長線上的一點，且AP=
AC.
（1）求證：AP與⊙O相切；
（2）如果AC=3，求PD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
分解因式，結果為 ． 
∥
，EA是
的平分線，若
，則
，
, 
，垂足分別為
、
，聯結AC、DF，∠A=∠D.
.
中，
， 
，
，點
在四邊形
的距離為
，則點