Question

6．如圖，在Rt△ABC中，∠C=90°，AC=4，BC=3．
（1）求作⊙P，使圓心P在BC上，⊙P與AC、AB都相切；（要求：尺規作圖，不寫作法，保留作圖痕跡）
（2）求⊙P的半徑．

Answer 1

分析 （1）作∠BAC的平分線交BC于P點，然后以點P為圓心，PC為半徑作圓即可得到⊙P；
（2）設⊙P與AB相切于點D，連接PD，則PD⊥AB，如圖，先判斷AC為⊙P的切線，則根據切線長定理得到AD=AC=4，所以BD=AB-AD=1，再△BPD∽△BAC，然后利用相似比計算出PD即可．

解答 解：（1）如圖，⊙P為所作；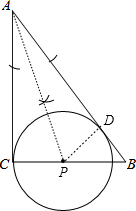

（2）設⊙P與AB相切于點D，連接PD，則PD⊥AB，如圖，
∵∠ACP=90°，
∴AC為⊙P的切線，
∴AD=AC=4，
∴BD=AB-AD=1，
∵∠PDB=∠ACB=90°，∠B=∠B，
∴△BPD∽△BAC，
∴$\frac{PD}{AC}$=$\frac{BD}{BC}$，即$\frac{PD}{4}$=$\frac{1}{3}$，解得PD=$\frac{4}{3}$，
即⊙P的半徑為$\frac{4}{3}$．

點評 本題考查了作圖-復雜作圖：復雜作圖是在五種基本作圖的基礎上進行作圖，一般是結合了幾何圖形的性質和基本作圖方法．解決此類題目的關鍵是熟悉基本幾何圖形的性質，結合幾何圖形的基本性質把復雜作圖拆解成基本作圖，逐步操作．也考查了切線的性質．