
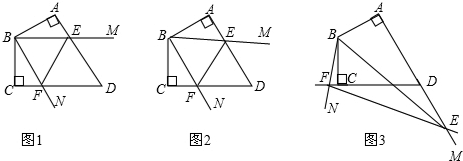
分析 (1)如圖1中,根據△ABE≌△CBF可證△BEF是等邊三角形,即可解題;
(2)①如圖2中,結論仍然成立.證明△EBF≌△KBF,即可得EF=CK+CF,可證AE+CF=EF;
③如圖3中,結論不成立,猜想猜想AE-CF=EF.在DC的延長線上取點K,使CK=AE,連接BK證明△EBF≌△KBF,即可得AE-CF=EF.
解答 解:(1)如圖1中,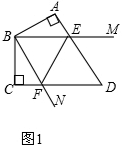
在△ABE和△CBF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠BCF}\\{AE=CF}\end{array}\right.$,
∴△ABE≌△CBF(SAS).
∴BE=BF,∴∠ABE=∠CBF=$\frac{1}{2}$(∠ABC-∠MBN)=$\frac{1}{2}$(120°-60°)=30°.
∴AE=$\frac{1}{2}$BE,CF=$\frac{1}{2}$BF,
△BEF是等邊三角形.
∴BE=BF=EF.
∴AE+CF=$\frac{1}{2}$BE+$\frac{1}{2}$BF=EF;
(2)①如圖2中,結論仍然成立.理由如下:
延長DC至K點使得CK=AE,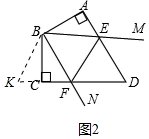
在△ABE和△CBK中,
$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠BCK}\\{AE=CK}\end{array}\right.$,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC,
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,
即∠KBE=120°,
∵∠EBF=60°,
∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
$\left\{\begin{array}{l}{BK=BE}\\{∠KBF=∠EBF}\\{BF=BF}\end{array}\right.$,
∴△EBF≌△KBF(SAS).
∴EF=KF.
∴EF=CK+CF.
∴AE+CF=EF;
③如圖3,結論不成立.猜想AE-CF=EF,理由如下:
證明如下:在DC的延長線上取點K,使CK=AE,連接BK.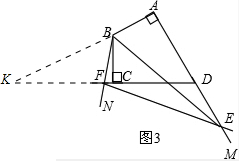
在△ABE和△CBK中,
$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠BCK}\\{AE=CK}\end{array}\right.$,
∴△ABE≌△CBK(SAS).
∴BE=BK,∠ABE=∠KBC,
∵∠ABE+∠CBE=120°,
∴∠KBC+∠CBE=120°,
即∠KBE=120°.
∵∠EBF=60°,
∴∠KBF=∠EBF=60°.
在△EBF和△KBF中,
$\left\{\begin{array}{l}{BE=BK}\\{∠KBF=∠EBF}\\{BF=BF}\end{array}\right.$,
∴△EBF≌△KBF(SAS),
∴EF=KF,
∴EF=CK-CF.
∴AE-CF=EF.
點評 本題考查了全等三角形的判定和性質,等邊三角形的性質等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,屬于中考常考題型.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
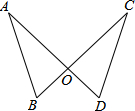 如圖AB=CD,AD與BC交于點O,要使△AOB≌△COD,不添加輔助線則需條件是( )
如圖AB=CD,AD與BC交于點O,要使△AOB≌△COD,不添加輔助線則需條件是( )| A. | AO=CO | B. | BO=DO | C. | BC=AD | D. | ∠A=∠C |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,已知矩形ABCD,AB=1,又ABEF是正方形,若矩形CDEF與矩形ABCD相似,則AD長為:$\frac{\sqrt{5}+1}{2}$.
如圖,已知矩形ABCD,AB=1,又ABEF是正方形,若矩形CDEF與矩形ABCD相似,則AD長為:$\frac{\sqrt{5}+1}{2}$.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
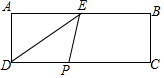 已知,如圖,在長方形ABCD中,AB=8,AD=3,點E是AB的中點,點P是CD上的動點,點B關于直線PE的對稱點為M,問:當CP的長為3或$\sqrt{7}$時,點M恰好落在△DEP的邊上.
已知,如圖,在長方形ABCD中,AB=8,AD=3,點E是AB的中點,點P是CD上的動點,點B關于直線PE的對稱點為M,問:當CP的長為3或$\sqrt{7}$時,點M恰好落在△DEP的邊上.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 先向左平移1個單位,再向上平移4個單位 | |
| B. | 先向右平移1個單位,再向上平移4個單位 | |
| C. | 先向左平移1個單位,再向下平移4個單位 | |
| D. | 先向右平移1個單位,再向下平移4個單位 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1.5cm 3.9cm 2.3cm | B. | 3.5cm 7.1cm 3.6cm | ||
| C. | 6cm 1cm 6cm | D. | 4cm 10cm 4cm |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com