
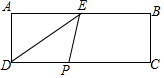
 已知,如圖,在長方形ABCD中,AB=8,AD=3,點E是AB的中點,點P是CD上的動點,點B關于直線PE的對稱點為M,問:當CP的長為3或$\sqrt{7}$時,點M恰好落在△DEP的邊上.
已知,如圖,在長方形ABCD中,AB=8,AD=3,點E是AB的中點,點P是CD上的動點,點B關于直線PE的對稱點為M,問:當CP的長為3或$\sqrt{7}$時,點M恰好落在△DEP的邊上. 分析 分兩種情形討論即可①如圖1中,當點M在DE上時,②如圖2中,當點M在DP上時.
解答 解:①如圖1中,當點M在DE上時,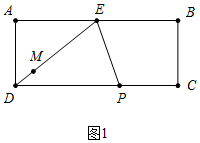
∵四邊形ABCD是長方形,
∴AB∥CD,AB=CD=8,
∴∠BEP=∠EPD,
∵∠BEP=∠DEP,
∴∠DEP=∠DPE,
∴DE=DP,
在Rt△ADE中,∵AD=3,AE=4,
∴DP=DE=$\sqrt{A{D}^{2}+A{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴PC=CD-DP=8-5=3.
②如圖2中,當點M在DP上時,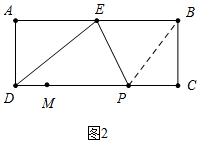
∵AB∥CD,
∴∠BEP=∠EPD,
∵∠EPD=∠EPB,
∴∠BEP=∠BPE,
∴EB=PB=4,
在Rt△PBC中,∵PB=4,BC=3,
∴PC=$\sqrt{P{B}^{2}-B{C}^{2}}$=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$.
綜上所述,PC的長為3或$\sqrt{7}$.
故答案為3或$\sqrt{7}$.
點評 本題考查矩形的性質、軸對稱的性質、等腰三角形的判定和性質、勾股定理等知識,解題的關鍵是等腰三角形的判定和性質的應用,屬于中考常考題型.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:填空題
 如圖,在直角坐標系中,以點C為圓心,2為半徑作圓,交x軸于A,B兩點,點A(1-$\sqrt{3}$,0),B(1+$\sqrt{3}$,0),函數y=$\frac{k}{x}$的圖象過點C,則k=1.
如圖,在直角坐標系中,以點C為圓心,2為半徑作圓,交x軸于A,B兩點,點A(1-$\sqrt{3}$,0),B(1+$\sqrt{3}$,0),函數y=$\frac{k}{x}$的圖象過點C,則k=1.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com