
【題目】已知數軸上有A,B,C三點,分別代表﹣36,﹣10,10,兩只電子螞蟻甲,乙分別從A,C兩點同時相向而行,甲的速度為4個單位/秒.
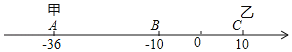
(1)問多少秒后,甲到A,B,C的距離和為60個單位?
(2)若乙的速度為6個單位/秒,兩只電子螞蟻甲,乙分別從A,C兩點同時相向而行,問甲,乙在數軸上的哪個點相遇?
(3)在(1)(2)的條件下,當甲到A、B、C的距離和為60個單位時,甲調頭返回.問甲,乙還能在數軸上相遇嗎?若能,求出相遇點;若不能,請說明理由.
【答案】(1)經過3s或10s后,甲到A,B,C的距離和為60個單位;(2)甲,乙在數軸上的點﹣17.6相遇;(3)甲從A向右運動3秒時返回,能在數軸上與乙相遇,相遇點表示的數為﹣56.
【解析】
(1)設x秒后甲到A,B,C三點的距離之和為60個單位,分甲應為于AB或BC之間兩種情況討論即可求解;
(2)可設x秒后甲與乙相遇,根據甲與乙的路程和為46,可列出方程求解即可;
(3)設y秒后甲到A,B,C三點的距離之和為60個單位,分甲應為于AB或BC之間兩種情況討論即可求解.
解:(1)設x秒后,甲到A,B,C的距離和為60個單位.
B點距A,C兩點的距離為26+20=46<60,
A點距B、C兩點的距離為26+46=72>60,
C點距A、B的距離為46+20=66>40,
故甲應位于AB或BC之間.
①AB之間時:4x+(26﹣4x)+(26﹣4x+20)=60,x=3;
②BC之間時:4x+(4x﹣26)+(46﹣4x)=60,x=10,
綜上所述,經過3s或10s后,甲到A,B,C的距離和為60個單位;
(2)設ts后甲與乙相遇
4t+6t=46,
解得:x=4.6,
4×4.6=18.4,﹣36+18.4=﹣17.6
答:甲,乙在數軸上的點﹣17.6相遇;
(3)設y秒后甲到A,B,C三點的距離之和為60個單位,
①甲從A向右運動3秒時返回,此時甲、乙表示在數軸上為同一點,所表示的數相同.
甲表示的數為:﹣36+4×3﹣4y;乙表示的數為:10﹣6×3﹣6y,
依據題意得:﹣36+4×3﹣4y=10﹣6×3﹣6y,
解得:y=8,
相遇點表示的數為:﹣36+4×3﹣4y=﹣56(或:10﹣6×3﹣6y=﹣56),
②甲從A向右運動10秒時返回,設y秒后與乙相遇.
甲表示的數為:﹣36+4×10﹣4y;乙表示的數為:10﹣6×10﹣6y,
依據題意得:﹣36+4×10﹣4y=10﹣6×10﹣6y,
解得:y=﹣27(不合題意舍去),
即甲從A向右運動3秒時返回,能在數軸上與乙相遇,相遇點表示的數為﹣56.


 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:初中數學 來源: 題型:
【題目】撫順某中學為了解八年級學生的體能狀況,從八年級學生中隨機抽取部分學生進行體能測試,測試結果分為A,B,C,D四個等級.請根據兩幅統計圖中的信息回答下列問題:
(1)本次抽樣調查共抽取了多少名學生?
(2)求測試結果為C等級的學生數,并補全條形圖;
(3)若該中學八年級共有700名學生,請你估計該中學八年級學生中體能測試結果為D等級的學生有多少名?
(4)若從體能為A等級的2名男生2名女生中隨機的抽取2名學生,做為該校培養運動員的重點對象,請用列表法或畫樹狀圖的方法求所抽取的兩人恰好都是男生的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
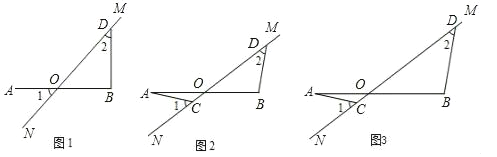
【題目】在圖1至圖3中,直線MN與線段AB相交于點O,∠1=∠2=45°.
(1)如圖1,若AO=OB,請寫出AO與BD的數量關系和位置關系;
(2)將圖1中的MN繞點O順時針旋轉得到圖2,其中AO=OB.求證:AC=BD,AC⊥BD;
(3)將圖2中的OB拉長為AO的k倍得到圖3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某書店準備購進甲、乙兩種圖書共100本,購書款不高于1118元,預這100本圖書全部售完的利潤不低于1100元,兩種圖書的進價、售價如表所示:
甲種圖書 | 乙種圖書 | |
進價(元/本) | 8 | 14 |
售價(元/本) | 18 | 26 |
請回答下列問題:
(1)書店有多少種進書方案?
(2)在這批圖書全部售出的條件下,(1)中的哪種方案利潤最大?最大利潤是多少?(請你用所學的一次函數知識來解決)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:如圖1,⊙![]() 與直線
與直線![]() 都相切.不論⊙
都相切.不論⊙![]() 如何轉動,直線
如何轉動,直線![]() 之間的距離始終保持不變(等于⊙
之間的距離始終保持不變(等于⊙![]() 的半徑).我們把具有這一特性的圖形稱為“等寬曲線”.圖2是利用圓的這一特性的例子.將等直徑的圓棍放在物體下面,通過圓棍滾動,用較小的力就可以推動物體前進.據說,古埃及就是利用只有的方法將巨石推到金字塔頂的.
的半徑).我們把具有這一特性的圖形稱為“等寬曲線”.圖2是利用圓的這一特性的例子.將等直徑的圓棍放在物體下面,通過圓棍滾動,用較小的力就可以推動物體前進.據說,古埃及就是利用只有的方法將巨石推到金字塔頂的.

拓展應用:如圖3所示的弧三角形(也稱為萊洛三角形)也是“等寬曲線”.如圖4,夾在平行線![]() 之間的萊洛三角形無論怎么滾動,平行線間的距離始終不變.若直線
之間的萊洛三角形無論怎么滾動,平行線間的距離始終不變.若直線![]() 之間的距離等于
之間的距離等于![]() ,則萊洛三角形的周長為
,則萊洛三角形的周長為 ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有依次3個數:2、9、7.對任意相鄰的兩個數,都用右邊的數減去左邊的數,所得之差寫在這兩個數之間,可產生一個新數串:2、7、9、-2、7,這稱為第1次操作,做第2次同樣的操作后也可以產生一個新數串:2、5、7、2、9、-11、-2、9、7,繼續依次操作下去,問從數串2、9、7開始操作第20次后所產生的那個數串的所有數之和是___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道,任意一個正整數n都可以進行這樣的分解:n=p×q(p,q是正整數,且p≤q),在n的所有這種分解中,如果p,q兩因數之差的絕對值最小,我們就稱p×q是n的最佳分解,并規定:F(n)=![]() ,例如12可以分解成1×12,2×6或3×4,因為12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因為12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=![]() .
.
(1)如果一個正整數a是另外一個正整數b的平方,我們稱正整數a是完全平方數,求證:對任意一個完全平方數m,總有F(m)=1.
(2)如果一個兩位正整數t,t=10x+y(1≤x≤y≤9,x,y為自然數),交換其個位上的數與十位上的數得到的新數減去原來的兩位正整數所得的差為18,那么我們稱這個數t為“吉祥數”,求所有“吉祥數”中F(t)的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD的外側作等腰△ABE,AE=BE,連接ED、EC.
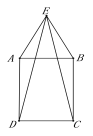
(1)求證:ED=EC.
(2)用無刻度的直尺作出△EDC中DC邊上的高EH.(不寫作法,保留作圖的痕跡)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com