Question

如圖，在平面直角坐標系中，直線l平行x軸，交y軸于點A，第一象限內的點B在l上，連結OB，動點P滿足∠APQ=90°，PQ交x軸于點C．

（1）當動點P與點B重合時，若點B的坐標是（2，1），求PA的長．

（2）當動點P在線段OB的延長線上時，若點A的縱坐標與點B的橫坐標相等，求PA：PC的值．

（3）當動點P在直線OB上時，點D是直線OB與直線CA的交點，點E是直線CP與y軸的交點，若∠ACE=∠AEC，PD=2OD，求PA：PC的值．

 

 

Answer 1

（1）2；（2）1：1；（3）或．

【解析】

試題分析：（1）易得點P的坐標是（2，1），即可得到PA的長．

（2）易證∠AOB=45°，由角平分線的性質可得PA=PC，然后通過證明△ANP≌△CMP即可求出PA：PC的值．

（3）可分點P在線段OB的延長線上及其反向延長線上兩種情況進行討論．易證PA：PC=PN：PM，設OA=x，只需用含x的代數式表示出PN、PM的長，即可求出PA：PC的值．

試題解析：【解析】
（1）∵點P與點B重合，點B的坐標是（2，1），∴點P的坐標是（2，1）．∴PA的長為2．

（2）如答圖1，過點P作PM⊥x軸，垂足為M，過點P作PN⊥y軸，垂足為N，

∵點A的縱坐標與點B的橫坐標相等，∴OA=AB．

∵∠OAB=90°，∴∠AOB=∠ABO=45°．

∵∠AOC=90°，∴∠POC=45°．

∵PM⊥x軸，PN⊥y軸，∴PM=PN，∠ANP=∠CMP=90°．∴∠NPM=90°．

∵∠APC=90°．∴∠APN=90°﹣∠APM=∠CPM．

在△ANP和△CMP中，∵∠APN=∠CPM，PN=PM，∠ANP=∠CMP，

∴△ANP≌△CMP．∴PA=PC．∴PA：PC的值為1：1．

（3）①若點P在線段OB的延長線上，如答圖2，過點P作PM⊥x軸，垂足為M，過點P作PN⊥y軸，垂足為N，PM與直線AC的交點為F．

∵∠APN=∠CPM，∠ANP=∠CMP，∴△ANP∽△CMP．∴．

∵∠ACE=∠AEC，∴AC=AE．

∵AP⊥PC，∴EP=CP．

∵PM∥y軸，∴AF=CF，OM=CM．∴FM=OA．

設OA=x，∵PF∥OA，∴△PDF∽△ODA．∴.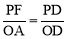

∵PD=2OD，∴PF=2OA=2x，FM=x．∴PM=x．

∵∠APC=90°，AF=CF，∴AC=2PF=4x．

∵∠AOC=90°，∴OC=x．

∵∠PNO=∠NOM=∠OMP=90°，∴四邊形PMON是矩形．∴PN=OM=x．

∴PA：PC=PN：PM=x：x=．

②若點P在線段OB的反向延長線上，如答圖3，過點P作PM⊥x軸，垂足為M，過點P作PN⊥y軸，垂足為N，PM與直線AC的交點為F．

同理可得：PM=x，CA=2PF=4x，OC=x．

∴PN=OM=OC=x．

∴PA：PC=PN：PM=x：x=．

綜上所述：PA：PC的值為或．

考點：1.單動點問題；2.全等三角形的判定和性質；3.角平分線的性質；4.等腰三角形的判定和性質；5.勾股定理；6.矩形的判定和性質；7.平行線分線段成比例；8.相似三角形的判定和性質；9.分類思想的應用．