
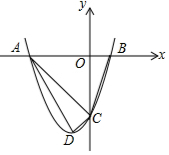
 已知:二次函數y=mx2+2mx-3m的圖象與x軸交于A、B兩點(點A在左,點B在右),與y軸交于點C(m>0),頂點為D.當m取何值時,以A、D、C三點為頂點的三角形與△OBC相似?
已知:二次函數y=mx2+2mx-3m的圖象與x軸交于A、B兩點(點A在左,點B在右),與y軸交于點C(m>0),頂點為D.當m取何值時,以A、D、C三點為頂點的三角形與△OBC相似? 分析 分兩種情形討論即可:①當∠ACD=90°時,作DH⊥OC于H.由△AOC∽△CHD,推出$\frac{OA}{CH}$=$\frac{OC}{DH}$,可得$\frac{3}{m}$=$\frac{3m}{1}$,解得m=1或-1(舍棄),由此即可判斷.②當∠ADC=90°時,作DH⊥OC于H,AE⊥DH于E.由△AED∽△DHC,可得$\frac{AE}{DH}$=$\frac{DE}{CH}$,可得$\frac{4m}{1}$=$\frac{2}{m}$,求得m=$\frac{\sqrt{2}}{2}$或-$\frac{\sqrt{2}}{2}$(舍棄),由此即可解決問題.
解答 解:①當∠ACD=90°時,作DH⊥OC于H.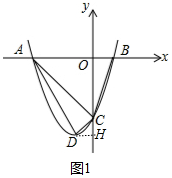
由題意可知A(-3,0),B(1,0),C(0,-3m),D(-1,-4m),
∵∠ACO+∠CAO=90°,∠ACO+∠DCH=90°,
∴∠CAO=∠DCH,∵∠AOC=∠DHC=90°,
∴△AOC∽△CHD,
∴$\frac{OA}{CH}$=$\frac{OC}{DH}$,
∴$\frac{3}{m}$=$\frac{3m}{1}$,
∴m=1或-1(舍棄),
∴C(0,-3),D(-1,-4),
∴OA=3$\sqrt{2}$,CD=$\sqrt{2}$,
∴$\frac{AC}{CD}$=$\frac{OC}{OB}$=3,
∴$\frac{AC}{OC}$=$\frac{CD}{OB}$,∵∠ACD=∠BOC=90°,
∴△BOC∽△DCA.
②當∠ADC=90°時,作DH⊥OC于H,AE⊥DH于E.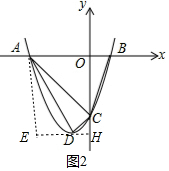
由△AED∽△DHC,可得$\frac{AE}{DH}$=$\frac{DE}{CH}$,
∴$\frac{4m}{1}$=$\frac{2}{m}$,
∴m=$\frac{\sqrt{2}}{2}$或-$\frac{\sqrt{2}}{2}$(舍棄),
∴AE=2$\sqrt{2}$,AD=2$\sqrt{3}$,DC=$\frac{\sqrt{6}}{2}$,
顯然此時△ADC與△OBC不相似.
綜上所述,m=1時,以A、D、C三點為頂點的三角形與△OBC相似.
點評 本題考查相似三角形的判定和性質、拋物線與坐標軸的交點問題、勾股定理等知識,解題的關鍵是靈活運用所學知識解決問題,學會用方程的思想思考問題,屬于中考常考題型.


 備戰中考寒假系列答案
備戰中考寒假系列答案科目:初中數學 來源: 題型:選擇題
| A. | 對學校的同學發放問卷進行調查 | |
| B. | 對在路邊行走的學生隨機發放問卷進行調查 | |
| C. | 對在圖書館里看書的人發放問卷進行調查 | |
| D. | 對在路邊行走的路人隨機發放問卷進行調查 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
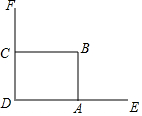 某縣扶貧開發辦公室為幫助該縣貧困戶開發經濟、發展生產、特為貧困戶建設養雞舍及圍欄.在為某農戶修建雞舍時,該農戶想借助如圖所示的直角舊墻角,用22米長的圍欄(全部用完)圍成一個矩形雞舍ABCD,點C在墻DF(墻DF的長為11米)上,點A在墻DE(墻DE足夠長)上.(圍欄只圍AB,BC兩邊)
某縣扶貧開發辦公室為幫助該縣貧困戶開發經濟、發展生產、特為貧困戶建設養雞舍及圍欄.在為某農戶修建雞舍時,該農戶想借助如圖所示的直角舊墻角,用22米長的圍欄(全部用完)圍成一個矩形雞舍ABCD,點C在墻DF(墻DF的長為11米)上,點A在墻DE(墻DE足夠長)上.(圍欄只圍AB,BC兩邊)查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | -1°C | B. | 0°C | C. | 1°C | D. | -2°C |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 45.5°=45°30′ | B. | 3a+b=3ab | C. | -$\frac{1}{2}$>-$\frac{1}{3}$ | D. | a3+a2=a5 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 任意拋擲一枚圖釘,結果針尖朝上 | |
| B. | 任意拋擲一枚均勻的骰子,骰子停止轉動后,朝上的一面的點數為1 | |
| C. | 連結⊙O的一條弦的中點和圓心的直線垂直這條弦 | |
| D. | 在一張紙上畫兩個三角形,這兩個三角形相似 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com