
分析 (1)根據(jù)題意得到w(元)關(guān)于n(本)的函數(shù)關(guān)系式,可得到一個關(guān)于n的不等式組,可求出n的取值范圍,再結(jié)合花費(fèi)的函數(shù)式,可求出x的具體數(shù)值;
(2)結(jié)合花費(fèi)的函數(shù)式,可求出x的具體數(shù)值;
(3)根據(jù)a的取值范圍即可得到結(jié)論.
解答 解:(1)依題意得:w=12n+8(30-n)
即w=4n+240
且n<$\frac{3}{4}$(30-n)和n≥$\frac{1}{4}$(30-n)
解得6≤n<12,
所以,w(元)關(guān)于n(本)的函數(shù)關(guān)系式為:w=4n+240
自變量n的取值范圍是6≤n<12,n為整數(shù),
(2)對于一次函數(shù)w=4n+240
∵w隨n的增大而增大,且6≤n<12,n為整數(shù),
故當(dāng)n為6時,w的值最小,
此時,30-n=30-6=24,w=4×6+240=264(元)
因此,當(dāng)買A種筆記本6本、B種筆記本24本時,所花費(fèi)用最少,為264元;
(3)設(shè)他們買A種筆記本x本,B種筆記本(30-x)本,
則w=(12-a)x+8(30-x),
∴w=(4-a)x+20,
∴當(dāng)a<4時,x=6,即買A種筆記本6本,B種筆記本24本,花費(fèi)最少,
當(dāng)a=4時,6≤x<12,買A種筆記本6到12本,B種筆記本24到18本,花費(fèi)=20,
當(dāng)a>4時,x=12,w最小,買A種筆記本12本,B種筆記本18本,花費(fèi)最少.
點(diǎn)評 本題考查一次函數(shù)的應(yīng)用,解題的關(guān)鍵是明確題意,找出所求問題需要的條件.


 智趣寒假作業(yè)云南科技出版社系列答案
智趣寒假作業(yè)云南科技出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 80° | B. | 100° | C. | 160° | D. | 170° |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
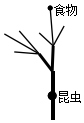 一只昆蟲在如圖所示的樹枝上尋覓食物,假定昆蟲在每個岔路口都會隨機(jī)地選擇一條路徑,則它獲得食物的概率是$\frac{1}{6}$.
一只昆蟲在如圖所示的樹枝上尋覓食物,假定昆蟲在每個岔路口都會隨機(jī)地選擇一條路徑,則它獲得食物的概率是$\frac{1}{6}$.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | x≠3 | B. | x<3 | C. | x≠3且x≠0 | D. | x≠0 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
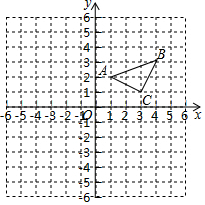 如圖所示,三角形ABC三個頂點(diǎn)A、B、C的坐標(biāo)分別為A (1,2)、B(4,3)、C(3,1).
如圖所示,三角形ABC三個頂點(diǎn)A、B、C的坐標(biāo)分別為A (1,2)、B(4,3)、C(3,1).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com