Question

14．已知直線l及位于其兩側(cè)的兩點A，B，如圖
（1）在圖①中的直線l上求一點P，使PA=PB；
（2）在圖②中的直線l上求一點Q，使直線l平分∠AQB；
（3）能否在直線l上找一點，使該點到點A，B的距離之差的絕對值最大？若能，直接指出該點的位置，若不能，請說明理由．

Answer 1

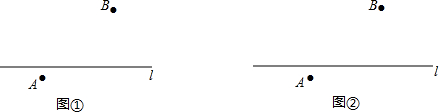
分析 （1）作線段AB的垂直平分線與l的交點即為所求．
（2）作點A關(guān)于l的對稱點A′，連接BA′并延長交l于點Q，點Q即為所求．
（3）圖2中的點Q即為所求．

解答 解：（1）連接AB作線段AB的垂直平分線MN，直線MN和直線l的交點為P，點P即為所求，見圖①．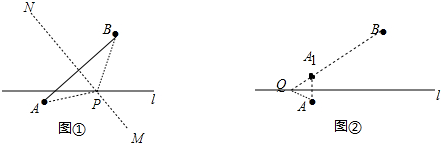
（2）作點A關(guān)于直線l的對稱點A₁，連接BA₁且延長交直線l于點Q，點Q即為所求，見圖②．
（3）圖②中的點Q即為所求，見圖③．
理由如下：在直線l上任意取一點Q₁，連接Q₁A₁，Q₁B，Q₁A，
∵A、A′關(guān)于直線l對稱，
∴Q₁A₁=Q₁A，
∵|Q₁A₁-Q₁B|≤A₁B（當Q₁與Q重合時等號成立），
∴|Q₁A-Q₁B|≤A₁B，
∵Q₁與Q重合時，
|QB-QA₁|=A₁B，
故點Q即為所求的點．

點評 本題考查線段的垂直平分線性質(zhì)、軸對稱的性質(zhì)以及三角形三邊關(guān)系等知識，靈活運用這些知識是解題的關(guān)鍵．