
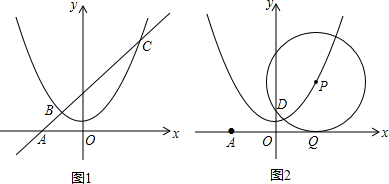
分析 (1)由拋物線與直線方程求得交點B、C的坐標,然后結合三角形的面積公式來求△OBC的面積;
(2)由拋物線與直線方程得到$\frac{1}{4}$x2-kx+1-4k,根據根與系數的關系求得xB+xC=4k,xB•xC=4(1-4k),易得點A的坐標,所以AM•AN=(xB+4)•(xC+4)=20,20是定值;
(3)當DA⊥l時D到l的距離最大.利用勾股定理和二次函數最值的求法進行解答即可.
解答 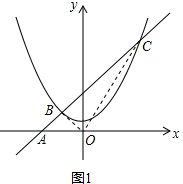 解:(1)如圖1,連接OB、OC.
解:(1)如圖1,連接OB、OC.
∵k=1,
∴直線l為y=x+4.
$由\left\{\begin{array}{l}y=x+4\\ y=\frac{1}{4}{x^2}+1\end{array}\right.得B(-2,2),C(6,10)$,E(0,4),
∴${S_{△OBC}}={S_{△OEB}}+{S_{△OEC}}=\frac{1}{2}OE|{x_B}|+\frac{1}{2}OE|{x_C}|=\frac{1}{2}×4×2+\frac{1}{2}×4×6=16$;
(2)$由\left\{\begin{array}{l}y=kx+4k\\ y=\frac{1}{4}{x^2}+1\end{array}\right.得\frac{1}{4}{x^2}-kx+1-4k=0$,
∴xB+xC=4k,xB•xC=4(1-4k)由y=kx+4k得A(-4,0),
∴AM•AN=(xB+4)•(xC+4)=xBxC+4(xB+xC)+16
=4(1-4k)+4×4k+16=20;
(3)如圖2,$設P(t,\frac{1}{4}{t^2}+1),作PF⊥y軸于F,連PD$.
∴$FD=\sqrt{P{D^2}-P{F^2}}=\sqrt{P{Q^2}-P{F^2}}=\sqrt{{{(\frac{1}{4}{t^2}+1)}^2}-t{\;}^2}=\frac{1}{4}{t^2}-1$,
∴$OD=OF-FD=\frac{1}{4}{t^2}+1-(\frac{1}{4}{t^2}-1)=2$,
∴$D(0,2),AD=2\sqrt{5}$.
∵直線l是繞點A旋轉,d≤DA,
∴當DA⊥l時D到l的距離最大,
∴$最大值是2\sqrt{5}$.
點評 本題考查了二次函數綜合題.解題時需要掌握拋物線與直線交點的求法,二次函數最值的求法,根與系數的關系以及三角形的面積計算.綜合性較強,難度適中.運用數形結合、方程思想是解題的關鍵.


科目:初中數學 來源:2016-2017學年河南省七年級下學期第一次月考(3月)數學試卷(解析版) 題型:單選題
如圖,DH∥EG∥BC,DC∥EF,那么與∠DCB相等的角的個數為( )

A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源:2016-2017學年江蘇省七年級下學期第一次月考數學試卷(解析版) 題型:單選題
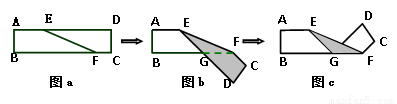
如圖a是長方形紙帶,∠DEF=15°,將紙帶沿EF折疊成圖b,再沿BF折疊成圖c,則圖c中的∠CFE的度數是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
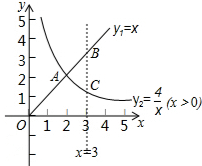 如圖所示,函數y1=x(x>0),y2=$\frac{4}{x}$(x>0)的圖象交于點A,與直線x=3分別交于B,C兩點,給出以下四個結論:
如圖所示,函數y1=x(x>0),y2=$\frac{4}{x}$(x>0)的圖象交于點A,與直線x=3分別交于B,C兩點,給出以下四個結論:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1298×104 | B. | 12.98×106 | C. | 1.298×107 | D. | 1.298×103 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com