
在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分線, DE⊥AB于點E.
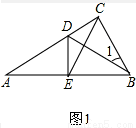
(1)如圖1,連接EC,求證:△EBC是等邊三角形;
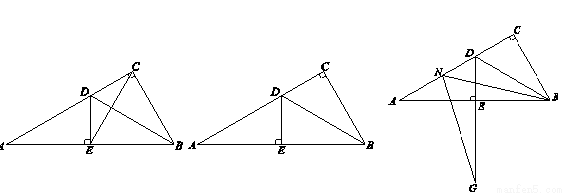
(2)點M是線段CD上的一點(不與點C,D重合),以BM為一邊,在BM的下方作∠BMG=60°,MG交DE延長線于點G.請你在圖2中畫出完整圖形,并直接寫出MD,DG與AD之間的數(shù)量關系;
(3)如圖3,點N是線段AD上的一點,以BN為一邊,在BN的下方作∠BNG=60°,NG交DE延長線于點G.試探究ND,DG與AD數(shù)量之間的關系,并說明理由.
(1)證明見解析:(2)AD=DG+DM.(3)AD=DG-DN.理由見解析.
【解析】
試題分析:(1)利用“三邊相等”的三角形是等邊三角形證得△EBC是等邊三角形;
(2)延長ED使得DN=DM,連接MN,即可得出△NDM是等邊三角形,利用△NGM≌△DBM即可得出BD=NG=DG+DM,再利用AD=BD,即可得出答案;
(3)利用等邊三角形的性質(zhì)得出∠H=∠2,進而得出∠DNG=∠HNB,再求出△DNG≌△HNB即可得出答案.
試題解析:(1)證明:如圖1所示:
在Rt△ABC中,∠ACB=90°,∠A=30°,
∴∠ABC=60°,BC=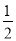 AB.
AB.
∵BD平分∠ABC,
∴∠1=∠DBA=∠A=30°.
∴DA=DB.
∵DE⊥AB于點E.
∴AE=BE=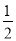 AB.
AB.
∴BC=BE.
∴△EBC是等邊三角形;
(2)結論:AD=DG+DM.
證明:如圖2所示:延長ED使得DN=DM,連接MN,
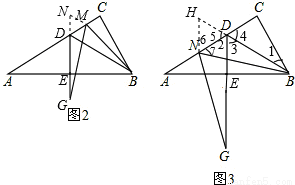
∵∠ACB=90°,∠A=30°,BD是△ABC的角平分線,DE⊥AB于點E,
∴∠ADE=∠BDE=60°,AD=BD,
又∵DM=DN,
∴△NDM是等邊三角形,
∴MN=DM,
在△NGM和△DBM中,
∵
∴△NGM≌△DBM,
∴BD=NG=DG+DM,
∴AD=DG+DM.
(3)結論:AD=DG-DN.
證明:延長BD至H,使得DH=DN.
由(1)得DA=DB,∠A=30°.
∵DE⊥AB于點E.
∴∠2=∠3=60°.
∴∠4=∠5=60°.
∴△NDH是等邊三角形.
∴NH=ND,∠H=∠6=60°.
∴∠H=∠2.
∵∠BNG=60°,
∴∠BNG+∠7=∠6+∠7.
即∠DNG=∠HNB.
在△DNG和△HNB中,

∴△DNG≌△HNB(ASA).
∴DG=HB.
∵HB=HD+DB=ND+AD,
∴DG=ND+AD.
∴AD=DG-ND.
考點:1.等邊三角形的判定與性質(zhì);2.全等三角形的判定與性質(zhì).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學 來源:2014-2015學年江蘇省附中七年級上學期期中考試數(shù)學試卷(解析版) 題型:填空題
意大利著名數(shù)學家斐波那契在研究兔子繁殖問題時,發(fā)現(xiàn)有這樣一組數(shù):1,1,2,3,5,8,13,…,其中從第三個數(shù)起,每一個數(shù)都等于它前面兩個數(shù)的和.現(xiàn)以這組數(shù)中的各個數(shù)作為正方形的邊長值構造正方形,再分別依次從左到右取2個、3個、4個、5個…正方形拼成如上長方形,若按此規(guī)律繼續(xù)作長方形,則序號為⑦的長方形周長是 .

查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年江蘇省南京江寧湖熟片七年級上學期期中檢測數(shù)學試卷(解析版) 題型:選擇題
下列各組數(shù)中,結果相等的是( )
A. 與
與
B. 與
與
C. 與
與
D. 與
與 .
.
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年江蘇省八年級12月月考數(shù)學試卷(解析版) 題型:填空題
一次函數(shù)y=﹣2x+1的圖象不經(jīng)過第 象限。
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年江蘇省八年級12月月考數(shù)學試卷(解析版) 題型:選擇題
點A(-3,-4)到原點的距離為( )
(A)3 (B)4 (C)5 (D)7
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年北京市八年級上學期期中檢測數(shù)學試卷(解析版) 題型:解答題
已知:如圖,A、B、C、D四點在同一直線上, AB=CD,AE∥BF且AE=BF.求證:EC=FD.

查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年北京市八年級上學期期中檢測數(shù)學試卷(解析版) 題型:填空題
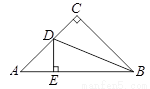
如圖,△ABC是等腰直角三角形,∠C=90°,BD平分∠CBA交AC于點D,DE⊥AB于E.若△ADB的面積為6,CD =2,則AB= .
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年四川省仁壽縣聯(lián)誼學校九年級上學期期中考試數(shù)學試卷(解析版) 題型:解答題
已知關于 的方程
的方程 ,
,
求證:(1)不論m為何值,方程是關于 的一元二次方程。
的一元二次方程。
(2)不論m為何值,方程總有兩個不相等的實數(shù)根。
查看答案和解析>>
科目:初中數(shù)學 來源:2014-2015學年江西省九年級上學期第二次月考數(shù)學試卷(解析版) 題型:填空題
一個底面直徑是80cm,母線長為90cm的圓錐的側面展開圖的圓心角的度數(shù)為 .
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com