
分析 (1)根據題意可以求得w關于n的函數關系式,由購買A筆記本的數量要少于B筆記本數量的$\frac{2}{3}$,但又不少于B筆記本數量的$\frac{1}{3}$,可以確定n的取值范圍;
(2)根據(1)中的函數關系式可以求得w的最小值及此時購買的A和B種兩種筆記本的數量.
解答 解:(1)依題意得:w=12n+8(30-n)
即w=4n+240
且n<$\frac{2}{3}$(30-n)和n≥$\frac{1}{3}$(30-n)
解得$\frac{15}{2}$≤n<12
所以,w(元)關于n(本)的函數關系式為:w=4n+240
自變量n的取值范圍是$\frac{15}{2}$≤n<12,n為整數;
(2)對于一次函數w=4n+240
∵w隨n的增大而增大,且$\frac{15}{2}$≤n<12,n為整數
故當n為8時,w的值最小
此時,30-n=30-8=22,w=4×8+240=272(元)
因此,當買A種筆記本8本、B種筆記本22本時,所花費用最少,為272元.
點評 本題考查了一次函數的應用,一元一次不等式的應用.此題利用了(總花費=A種筆記本的單位價×A的數量+B種筆記本的單位價×B的數量),還用到了解不等式組以及一次函數的有關性質(當k>0時,y隨x的增大而增大).


科目:初中數學 來源: 題型:解答題
 如圖,AB是半圓O的直徑,D是弧BC的中點,四邊形ABCD的對角線AD、BC交于點E,AC、BD的延長線交于點F
如圖,AB是半圓O的直徑,D是弧BC的中點,四邊形ABCD的對角線AD、BC交于點E,AC、BD的延長線交于點F查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
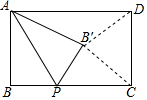 如圖,在矩形ABCD中,AB=a,BC=b,點P是BC上的一個動點,連接AP,把△PAB沿著AP翻折到△PB′C(點B′在矩形的內部),連接B′C,B′D.點P在整個運動過程中,若存在唯一的位置使得△B′CD為直角三角形,則a,b之間的數量關系是b=$\sqrt{2}$a.
如圖,在矩形ABCD中,AB=a,BC=b,點P是BC上的一個動點,連接AP,把△PAB沿著AP翻折到△PB′C(點B′在矩形的內部),連接B′C,B′D.點P在整個運動過程中,若存在唯一的位置使得△B′CD為直角三角形,則a,b之間的數量關系是b=$\sqrt{2}$a.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com