
【題目】定義:若線段![]() 上有一點
上有一點![]() ,當
,當![]() 時,則稱點
時,則稱點![]() 為線段
為線段![]() 的中點.已知數軸上
的中點.已知數軸上![]() ,
,![]() 兩點對應數分別為
兩點對應數分別為![]() 和
和![]() ,
,![]() ,
,![]() 為數軸上一動點,對應數為
為數軸上一動點,對應數為![]() .
.
(1)若點![]() 為線段
為線段![]() 的中點,則
的中點,則![]() 點對應的數
點對應的數![]() 為______.若
為______.若![]() 為線段
為線段![]() 的中點時則
的中點時則![]() 點對應的數
點對應的數![]() 為______.
為______.
(2)若點![]() 、點
、點![]() 同時向左運動,它們的速度都為1個單位長度/秒,與此同時點
同時向左運動,它們的速度都為1個單位長度/秒,與此同時點![]() 從-16處以2個單位長度/秒向右運動.
從-16處以2個單位長度/秒向右運動.
①設運動的時間為![]() 秒,直接用含
秒,直接用含![]() 的式子填空
的式子填空
![]() ______;
______;![]() ______.
______.
②經過多長時間后,點![]() 、點
、點![]() 、點
、點![]() 三點中其中一點是另外兩點的中點?
三點中其中一點是另外兩點的中點?
【答案】(1)1 ,10;(2)①![]() 或
或![]() (或者寫
(或者寫![]() ),
),![]() 或
或![]() (或者寫
(或者寫![]() ),②
),②![]() 或
或![]() 或
或![]()
【解析】
(1)根據線段中點的定義得出規律,再利用規律解答即可.
(2)①根據題意得出A、B、P表示的數,從而得出結論;
②分三種情況討論:若P為AB的中點,若A為BP的中點,若B為AP的中點,根據(1)所得結論列方程求解即可.
(1)∵P為線段AB的中點,∴AP=PB,
∴x-a=b-x,2x=a+b,
∴x=![]() ;
;
若B為線段AP的中點,則2b=a+x,解得:x=2b-a=8-(-2)=10.
故答案為:1,10.
(2)由題意得:A表示的數為-2-t,B表示的數為:4-t,P表示的數為:-16+2t.
①AP=|(-16+2t)-(-2-t)=|14-3t|,BP=|(-16+2t)-(4-t)|=|20-3t|,∴AP=-3t+14或14-3t;
BP=20-3t或3t-20.
故答案為:-3t+14或14-3t;20-3t或3t-20.
②分三種情況討論:
若P為AB的中點,則:2(-16+2t)=(-2-t)+(4-t),解得:t=![]() ;
;
若A為BP的中點,則:2(-2-t)=(-16+2t)+(4-t),解得:t=![]() ;
;
若B為AP的中點,則:2(4-t)=(-2-t)+(-16+2t),解得:t=![]() .
.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:
【題目】省教育廳決定在全省中小學開展“關注校車、關愛學生”為主題的交通安全教育宣傳周活動,某中學為了了解本校學生的上學方式,在全校范圍內隨機抽查了部分學生,將收集的數據繪制成如下兩幅不完整的統計圖(如圖所示),請根據圖中提供的信息,解答下列問題.
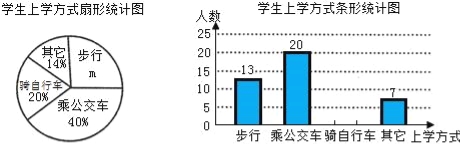
(1)m= %,這次共抽取 名學生進行調查;并補全條形圖;
(2)在這次抽樣調查中,采用哪種上學方式的人數最多?
(3)如果該校共有1500名學生,請你估計該校騎自行車上學的學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
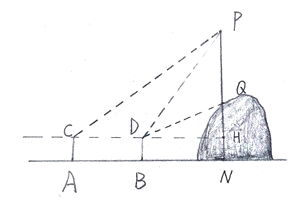
【題目】小明學校門前有座山,山上有一電線桿PQ,他很想知道電線桿PQ 的高度.于是,有一天,小明和他的同學小亮帶著側傾器和皮尺來到山腳下進行測量.測量方案如下:如圖,首先,小明站在地面上的點A處,測得電線桿頂端點P的仰角是45![]() ;然后小明向前走6米到達點B處,測得電線桿頂端點P和電線桿底端點Q的仰角分別是60
;然后小明向前走6米到達點B處,測得電線桿頂端點P和電線桿底端點Q的仰角分別是60![]() 和30
和30![]() ,設小明的眼睛到地面的距離為1.6米.請根據以上測量的數據,計算電線桿PQ的高度(結果精確到1米)參考數據:
,設小明的眼睛到地面的距離為1.6米.請根據以上測量的數據,計算電線桿PQ的高度(結果精確到1米)參考數據:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在8×8的正方形網格中,每個小正方形的頂點稱為格點,點A、B、C均在格點上,按下述要求畫圖并標注相關字母.

(1)畫線段AB,畫射線BC,畫直線AC;
(2)過點B畫線段BD⊥AC,垂足為點D;
(3)取線段AB的中點E,過點E畫BD的平行線,交AC于點F.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AB=AC,BE=CE,下面四個結論:①BP=CP;②AD⊥BC;③AE平分∠BAC;④∠PBC=∠PCB.其中正確的結論個數有( )個.
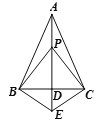
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝廠生產一種西裝和領帶,西裝每套定價280元,領帶每條定價40元,在促銷活動期間,該廠向客戶提供了兩種優惠方案(客戶只能選擇其中一種優惠方案):
方案一:買一套西裝送一條領帶;
方案二:西裝按原價的9折收費,領帶按原價的8折收費.
在促銷活動期間,某客戶要到該服裝廠購買![]() 套西裝,
套西裝,![]() 條領帶(
條領帶(![]() ).
).
(1)該客戶選擇兩種不同的方案所需費用分別是多少元?(用含![]() ,
,![]() 的式子表示并化簡)
的式子表示并化簡)
(2)若該客戶需要購買10套西裝,25條領帶,則他選擇哪種方案更劃算?
(3)若該客戶需要購買25套西裝,35條領帶,則他選擇哪種方案更劃算?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com