Question

16．如圖所示，AB∥CD，直線EF與AB相交于點E，與CD相交于點F，FH是∠EFD的角平分線，且與AB相交于點H，GF⊥FH交AB于點G（GF＞HP）．
（1）如圖①，求證：點E是GH的中點；
（2）如圖②，過點E作EP⊥AB交GF于點P，請判斷GP²=PF²+HF²是否成立？并說明理由；
（3）如圖③，在（1）的條件下，過點E作EP⊥EF交GF于點P，請猜想線段GP、PF、HF有怎樣的數量關系，請直接寫出你猜想的結果．

Answer 1

分析 （1）根據平行線的性質和角平分線的定義求得∠EHF=∠EFH，證得EF=EH，根據∠EFG+∠EFH=90°，∠EGF+∠EHF=90°，得出∠EFG=∠EGF，根據等角對等邊求得EG=EF，即可證得EH=EG，即E為HG的中點；
（2）連接PH，根據垂直平分線的性質得出PG=PH，在Rt△PFH中，根據勾股定理得：PH²=PF²+HF²，即可得到GP²=PF²+HF²；
（3）延長PE，使PE=EM，連接MH，MF，易證得△GPE≌△HME，從而得出GP=MH，∠1=∠2，進而證得EF垂直平分PM，根據垂直平分線的性質得出PF=MF，在RT△MHF中，MF²=MH²+FH²，即可得到PF²=GP²+FH²．

解答 （1）證明：∵AB∥CD，
∴∠EHF=∠HFD，
∵FH平分∠EFD，
∴∠EFH=∠HFD，
∴∠EHF=∠EFH，
∴EF=EH，
∵∠GFH=90°，
∴∠EFG+∠EFH=90°，∠EGF+∠EHF=90°，
∴∠EFG=∠EGF，
∴EG=EF，
∴EH=EG，
∴E為HG的中點；
（2）連接PH，如圖②：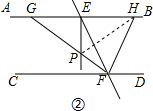
∵EP⊥AB，
又∵E是GH中點，
∴PE垂直平分GH，
∴PG=PH，
在Rt△PFH中，∠PFH=90°，
由勾股定理得：PH²=PF²+HF²，
∴GP²=PF²+HF²；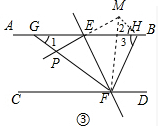 
（3）如圖③，延長PE，使PE=EM，連接MH，MF，
在△GPE和△HME中，
$\left\{\begin{array}{l}{GE=EH}\\{∠GEP=∠HEM}\\{PE=EM}\end{array}\right.$，
∴△GPE≌△HME（SAS），
∴GP=MH，∠1=∠2，
∵GF⊥FH，
∴∠1+∠3=90°，
∴∠2+∠3=90°，
∵EF⊥PM，PE=EM，
∴PF=MF，
在RT△MHF中，MF²=MH²+FH²，
∴PF²=GP²+FH²．

點評 本題考查了全等三角形的判定和性質，線段的垂直平分線的性質，等腰三角形的判定和性質，勾股定理的應用等，找出輔助線，構建等腰三角形是解題的關鍵．