
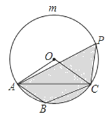
【題目】如圖,在△ABC中,∠ABC=120°,⊙O是△ABC的外接圓,點P是![]() 上的一個動點.
上的一個動點.
(1)求∠AOC的度數;
(2)若⊙O的半徑為2,設點P到直線AC的距離為x,圖中陰影部分的面積為y,求y與x之間的函數關系式,并寫出自變量x的取值范圍.\
【答案】(1)120°;(2)y=![]() ﹣
﹣![]() +
+![]() x(0≤x≤3)
x(0≤x≤3)
【解析】
(1)先根據圓內接四邊形的性質求出∠P的度數,再由圓周角定理即可得出結論;
(2)過點O作OH⊥AC于H,根據銳角三角函數的定義得出AH及OH的長,進而得出AC的長,用x表示出△APC的面積,再根據y=S扇形AOC-S△AOC+S△APC即可得出結論.
解:(1)∵∠ABC=120°,四邊形ABCP是圓內接四邊形,
∴∠P=180°﹣120°=60°,
∴∠AOC=2∠APC=120°;
(2)過點O作OH⊥AC于H,
∵∠AOC=120°,OC=OA=2,
∴∠OAC=30°,
∴AH=OAcos30°=2×![]() =
=![]() ,OH=
,OH=![]() OA=1,
OA=1,
∴AC=2AH=2![]() ,
,
∴S△APC=![]() ACx=
ACx=![]() x,
x,
∴y=S扇形AOC﹣S△AOC+S△APC=![]() ﹣
﹣![]() ×2
×2![]() ×1+
×1+![]() x=
x=![]() ﹣
﹣![]() +
+![]() x(0≤x≤3).
x(0≤x≤3).


科目:初中數學 來源: 題型:
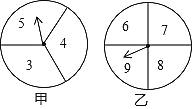
【題目】在一次數學興趣小組活動中,李燕和劉凱兩位同學設計了如圖所示的兩個轉盤做游戲(每個轉盤被分成面積相等的幾個扇形,并在每個扇形區域內標上數字).游戲規則如下:兩人分別同時轉動甲、乙轉盤,轉盤停止后, 若指針所指區域內兩數和等于 12,則李燕獲勝;若指針所指區域內兩數和等于 13,則劉凱獲勝(若指針停在等分線上,重轉一次,直到指針指向某一份內為止).
(1)請用列表或畫樹狀圖的方法表示出上述游戲中兩數和的所有可能的結果;
(2)游戲對雙方公平嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
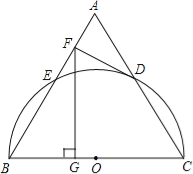
【題目】如圖,以等邊三角形ABC的BC邊為直徑畫半圓,分別交AB、AC于點E、D,DF是圓的切線,過點F作BC的垂線交BC于點G.若AF的長為2,則FG的長為
A. 4 B. ![]() C. 6 D.
C. 6 D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
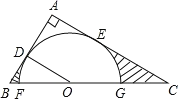
【題目】如圖,在Rt△ABC中,∠A=90°,O是BC邊上一點,以O為圓心的半圓與AB邊相切于點D,與AC、BC邊分別交于點E、F、G,連接OD,已知BD=2,AE=3,tan∠BOD=![]() .
.
(1)求證:AE是 O的切線;
(2)求圖中兩部分陰影面積的和.
查看答案和解析>>
科目:初中數學 來源: 題型:
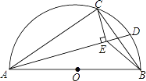
【題目】如圖,AB是半圓O的直徑,點C在半圓O上,AB=5cm,AC=4cm.D是弧BC上的一個動點(含端點B,不含端點C),連接AD,過點C作CE⊥AD于E,連接BE,在點D移動的過程中,BE的取值范圍是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點F,C是⊙O上兩點,且![]() ,連接AC,AF,過點C作CD⊥AF交AF延長線于點D,垂足為D.
,連接AC,AF,過點C作CD⊥AF交AF延長線于點D,垂足為D.
(1)求證:CD是⊙O的切線;
(2)若CD=2![]() ,求⊙O的半徑.
,求⊙O的半徑.

查看答案和解析>>
科目:初中數學 來源: 題型:
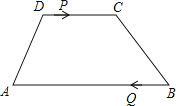
【題目】如圖,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,點P和Q同時從D、B出發,P由D向C運動,速度為每秒1cm,點Q由B向A運動,速度為每秒3cm,試求幾秒后,P、Q和梯形ABCD的兩個頂點所形成的四邊形是平行四邊形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市開展“環境治理留住青山綠水,綠色發展贏得金山銀山”活動,對其周邊的環境污染進行綜合治理.![]() 年對
年對![]() 、
、![]() 兩區的空氣量進行監測,將當月每天的空氣污染指數(簡稱:
兩區的空氣量進行監測,將當月每天的空氣污染指數(簡稱:![]() )的平均值作為每個月的空氣污染指數,并將
)的平均值作為每個月的空氣污染指數,并將![]() 年空氣污染指數繪制如下表.據了解,空氣污染指數
年空氣污染指數繪制如下表.據了解,空氣污染指數![]() 時,空氣質量為優:
時,空氣質量為優:![]() 空氣污染指數
空氣污染指數![]() 時,空氣質量為良:
時,空氣質量為良:![]() 空氣污染指數
空氣污染指數![]() 時,空氣質量為輕微污染.
時,空氣質量為輕微污染.
月份 地區 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)請求出![]() 、
、![]() 兩區的空氣污染指數的平均數;
兩區的空氣污染指數的平均數;
(2)請從平均數、眾數、中位數、方差等統計量中選兩個對![]() 區、
區、![]() 區的空氣質量進行有效對比,說明哪一個地區的環境狀況較好.
區的空氣質量進行有效對比,說明哪一個地區的環境狀況較好.
查看答案和解析>>
科目:初中數學 來源: 題型:
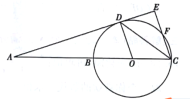
【題目】如圖,點D是⊙O上一點,直線AE經過點D,直線AB經過圓心O,交⊙O于B,C兩點,CE⊥AE,垂足為點E,交⊙O于點F,∠BCD=∠DCF
(1)求∠A+∠BOD的度數;
(2)若sin∠DCE=![]() ,⊙O的半徑為5,求線段AB的長.
,⊙O的半徑為5,求線段AB的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com