
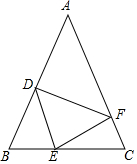
 如圖,在△ABC中,AB=AC,點D,E,F分別在AB,BC,AC邊上,且BE=CF,BD=CE.
如圖,在△ABC中,AB=AC,點D,E,F分別在AB,BC,AC邊上,且BE=CF,BD=CE.分析 (1)根據AB=AC可得∠B=∠C,即可求證△BDE≌△CEF,即可解題;
(2)根據全等三角形的性質得到∠CEF=∠BDE,于是得到∠DEF=∠B,根據等腰三角形的性質即可得到結論.
(3)由(1)知:△DEF是等腰三角形,DE=EF,由(2)知,∠DEF=∠B,于是得到結論.
解答 (1)證明:∵AB=AC,
∴∠B=∠C,
在△BDE和△CEF中,
∵$\left\{\begin{array}{l}{BE=CF}\\{∠B=∠C}\\{BD=CE}\end{array}\right.$
∴△BDE≌△CEF,
∴DE=EF,
∴△DEF是等腰三角形;
(2)解:∵∠DEC=∠B+∠BDE,
即∠DEF+∠CEF=∠B+∠BDE,
∵△BDE≌△CEF,
∴∠CEF=∠BDE,
∴∠DEF=∠B,
又∵在△ABC中,AB=AC,∠A=50°,
∴∠B=65°,
∴∠DEF=65°;
(3)解:由(1)知:△DEF是等腰三角形,DE=EF,
由(2)知,∠DEF=∠B,
而∠B不可能為直角,
∴△DEF不可能是等腰直角三角形.
點評 本題考查了全等三角形的判定和性質,等腰三角形的性質,熟練掌握全等三角形的判定和性質是解題的關鍵.


 課課優能力培優100分系列答案
課課優能力培優100分系列答案 優百分課時互動系列答案
優百分課時互動系列答案科目:初中數學 來源: 題型:解答題
 如圖,DB為半圓的直徑,A為BD延長線上一點,AC切半圓于點E,BC⊥AC于點C,交半圓于點F,已知BD=2,設AD=x,CF=y,求y關于x的函數解析式.
如圖,DB為半圓的直徑,A為BD延長線上一點,AC切半圓于點E,BC⊥AC于點C,交半圓于點F,已知BD=2,設AD=x,CF=y,求y關于x的函數解析式.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
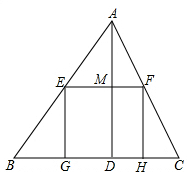 △ABC是一塊銳角三角形材料,邊BC=120cm,高AD=80cm,要把它加工成矩形零件EFGH,使矩形的一邊GH在BC上,其余兩個頂點E、F在AB,AC上,
△ABC是一塊銳角三角形材料,邊BC=120cm,高AD=80cm,要把它加工成矩形零件EFGH,使矩形的一邊GH在BC上,其余兩個頂點E、F在AB,AC上,查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{5}$是有理數 | B. | 面積為5的正方形邊長是$\sqrt{5}$ | ||
| C. | $\sqrt{5}$介于2和3之間 | D. | 在數軸上可以找到表示$\sqrt{5}$的點 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{16}{5}$ | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 10 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com