
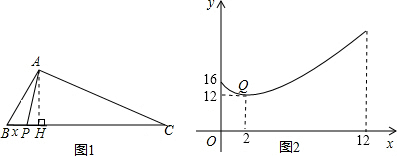
分析 (1)當AP⊥BC時可知AP2最小,由函數圖象可知AP2的值,可求得AP的長即AH的長,在△ABH中,利用三角函數定義可求得AB;
(2)當∠APB=90°時,由(1)利用直角三角形的性質可求得BP的長,當∠BAP=90°時,由直角三角形的性質可知BP=2AB,可求得答案.
解答 解:
(1)當AP⊥BC時可知AP2最小,
∵函數圖象中過Q點時函數值最小,
∴AH=$\sqrt{12}$=2$\sqrt{3}$,即BC邊上的高為2$\sqrt{3}$;
在Rt△ABH中,∠B=60°,
∴$\frac{AH}{AB}$=sin60°,即$\frac{2\sqrt{3}}{AB}$=$\frac{\sqrt{3}}{2}$,解得AB=4,
故答案為:4;2$\sqrt{3}$;
(2)當∠APB=90°時,在△ABP中,∠B=60°,
∴∠BAP=30°,∴BP=$\frac{1}{2}$AB=2;
當∠BAP=90°時,在△ABP中,∠B=60°,
∴∠APB=30°,
∴BP=2AB=8.
綜上可知當△ABP為直角三角形時,BP的長是2或8.
點評 本題為二次函數的綜合應用,涉及函數圖象與性質、三角函數定義、直角三角形的性質及分類討論思想等知識.在(1)中由圖象信息得出AH的長是解題的關鍵,在(2)中分兩種情況分別利用直角三角形的性質求得BP與AB的關系是解題的關鍵.本題考查知識較基礎,較易得分.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| 圖形 |  |  |  | … |
| 直線條數 | 2 | 3 | 4 | … |
| 最多交點個數 | 1 | 3=1+2 | 6=1+2+3 | … |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 在一個標準大氣壓下,加熱到100℃,水沸騰 | |
| B. | 拋一枚硬幣,正面朝上 | |
| C. | 某運動員射擊一次,擊中靶心 | |
| D. | 明天一定是晴天 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,∠MON=30°,且OP平分∠MON,過點P作PQ∥OM交ON于點Q.若點P到OM的距離為2,則OQ的長為( )
如圖,∠MON=30°,且OP平分∠MON,過點P作PQ∥OM交ON于點Q.若點P到OM的距離為2,則OQ的長為( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
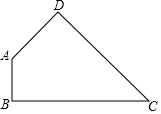 如圖,四邊形ABCD中,∠ABC=∠ADC=90°,∠C<90°.點E、F分別是BC、CD上的動點,滿足:△AEF的周長最小.
如圖,四邊形ABCD中,∠ABC=∠ADC=90°,∠C<90°.點E、F分別是BC、CD上的動點,滿足:△AEF的周長最小.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 3 | 2 | 1 | 0 | -1 | -2 |
| A. | x>0 | B. | x<0 | C. | x>1 | D. | x<1 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com