
【題目】某公司從2014年開始投入技術改進資金,經技術改進后,其產品的成本不斷降低,具體數據如下表:
年度 | 投入技改資金 | 產品成本 |
2014 |
|
|
2015 | 3 | 12 |
2016 | 4 | 9 |
2017 |
| 8 |
(1)分析表中數據,請從一次函數和反比例函數中確定一個函數表示其變化規律,直接寫出y與x的函數關系式;
(2)按照這種變化規律,若2018年已投入資金6萬元.
①預計2018年每件產品成本比2017年降低多少萬元?
②若計劃在2018年把每件產品成本降低到5萬元,則還需要投入技改資金多少萬元?
【答案】(1)![]() ;(2)
;(2)![]() 預計2018年每件產品成本比2017年降低2萬元;
預計2018年每件產品成本比2017年降低2萬元;![]() 還需要投入技改資金
還需要投入技改資金![]() 萬元.
萬元.
【解析】![]() 根據實際題意和數據特點分情況求解,根據排除法可知其為反比例函數,利用待定系數法求解即可;
根據實際題意和數據特點分情況求解,根據排除法可知其為反比例函數,利用待定系數法求解即可;
![]() 直接把
直接把![]() 萬元代入函數解析式即可求解;
萬元代入函數解析式即可求解;![]() 直接把
直接把![]() 代入函數解析式即可求解.
代入函數解析式即可求解.
![]() 設其為一次函數,解析式為
設其為一次函數,解析式為![]() ,
,
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
![]()
解得![]() ,
,![]()
![]() 一次函數解析式為
一次函數解析式為![]()
把![]() 時,
時,![]() 代入一次函數解析式,
代入一次函數解析式,
左邊![]() 右邊
右邊![]()
![]() 其不是一次函數
其不是一次函數![]()
同理![]() 其也不是二次函數
其也不是二次函數![]()
設其為反比例函數![]() 解析式為
解析式為![]()
當![]() 時,
時,![]() ,可得
,可得![]() ,
,
![]() 反比例函數是
反比例函數是![]()
驗證:當![]() 時,
時,![]() ,符合反比例函數
,符合反比例函數![]()
同理可驗證![]() 時,
時,![]() 成立
成立![]()
可用反比例函數![]() 表示其變化規律;
表示其變化規律;
![]()
![]() 當
當![]() 時,
時,![]() ,
,![]() ,
,
答:預計2018年每件產品成本比2017年降低2萬元;
![]() 當
當![]() 時,
時,![]() ,
, ![]() ,
,
答:還需要投入技改資金![]() 萬元.
萬元.


 一線名師提優試卷系列答案
一線名師提優試卷系列答案 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
【題目】已知5臺A型機器一天的產品裝滿8箱后還剩4個,7臺B型機器一天的產品裝滿11箱后還剩1個,每臺A型機器比B型機器一天多生產1個產品.
(1)求每箱裝多少個產品.
(2)3臺A型機器和2臺B型機器一天能生產多少個產品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展校園足球運動,某縣城區四校決定聯合購買一批足球運動裝備,市場調查發現:甲、乙兩商場以同樣的價格出售同種品牌的足球隊服和足球,已知每套隊服比每個足球多50元,兩套隊服與三個足球的費用相等.經洽談,甲商場的優惠方案是:每購買10套隊服,送1個足球;乙商場的優惠方案是:若購買隊服超過80套,則購買足球打八折.
(1)每套隊服和每個足球的價格分別是多少?
(2)若城區四校聯合購買100套隊服和a個足球,請用含a的式子分別表示出到甲商場和乙商場購買裝備所需的費用.
(3)假如你是本次購買任務的負責人,你認為到哪家商場購買比較合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某養殖戶每年的養殖成本包括固定成本和可變成本,其中固定成本每年均為4萬元,可變成本逐年增長,已知該養殖戶第一年的可變成本為2.6萬元,設可變成本平均每年增長的百分率為![]()
(1)用含x的代數式表示低3年的可變成本為 萬元;
(2)如果該養殖戶第3年的養殖成本為7.146萬元,求可變成本平均每年的增長百分率x.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的運算程序中,若開始輸入的x值為48,我們發現第1次輸出的結果為24,第2次輸出的結果為12,…第2019次輸出的結果為( )

A. 3 B. 6 C. 12 D. 24
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市團委舉行以“我的中國夢”為主題的知識競賽,甲、乙兩所學校的參賽人數相等,比賽結束后,發現學生成績分別為![]() 分,
分,![]() 分,
分,![]() 分,
分,![]() 分,并根據統計數據繪制了如下不完整的統計圖表:
分,并根據統計數據繪制了如下不完整的統計圖表:
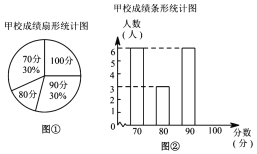
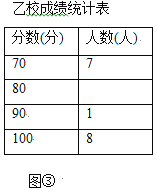
(1)乙學校的參賽人數是 人;
(2)在圖①中,“![]() 分”所在扇形的圓心角度數為 ;
分”所在扇形的圓心角度數為 ;
(3)請你將圖②補充完整;
(4)求乙校成績的平均分;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCB1中,AB=1,AB與直線l的夾角為30°,延長CB1交直線l于點A1 , 作正方形A1B1C1B2 , 延長C1B2交直線l于點A2 , 作正方形A2B2C2B3 , 延長C2B3交直線l于點A3 , 作正方形A3B3C3B4 , …,依此規律,則A2016A2017= . 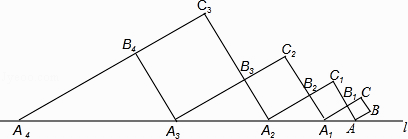
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,以AB為直徑的⊙O交BC于點M,MN⊥AC于點N. 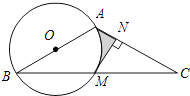
(1)求證:MN是⊙O的切線;
(2)若∠BAC=120°,AB=2,求圖中陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com