【題目】如圖，正方形ABCB1中，AB=1，AB與直線l的夾角為30°，延長CB1交直線l于點A1 ， 作正方形A1B1C1B2 ， 延長C1B2交直線l于點A2 ， 作正方形A2B2C2B3 ， 延長C2B3交直線l于點A3 ， 作正方形A3B3C3B4 ， …，依此規律，則A2016A2017= ．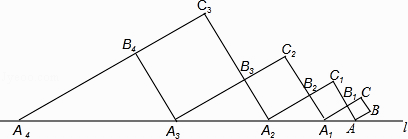 
【答案】2×31008
【解析】解：∵四邊形ABCB1是正方形， ∴AB=AB1 ， AB∥CB1 ，
∴AB∥A1C，
∴∠CA1A=30°，
∴A1B1= 
，AA1=2，
∴A1B2=A1B1= ，
∴A1A2=2 ，
同理：A2A3=2（ ）2 ，
A3A4=2（ ）3 ，
…
∴AnAn+1=2（ ）n ，
∴A2016A2017=2（ ）2016=2×31008 ．
故答案為：2×31008 ．
由四邊形ABCB1是正方形，得到AB=AB1 ， AB∥CB1 ， 于是得到AB∥A1C，根據平行線的性質得到∠CA1A=30°，解直角三角形得到A1B1= ，AA1=2，同理：A2A3=2（ ）2 ， A3A4=2（ ）3 ， 找出規律AnAn+1=2（ ）n ， 答案即可求出．
口算題卡加應用題集訓系列答案
綜合自測系列答案科目：初中數學 來源： 題型：
【題目】如圖，直線
與
軸、
軸分別交于
，點
的坐標為
，
是直線在第一象限內的一個動點
（1）求⊿
的面積
與的函數解析式，并寫出自變量的取值范圍？
（2）過點
作
軸于點
, 作
軸于點
,連接
,是否存在一點使得的長最小，若存在，求出的最小值；若不存在，請說明理由 ？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某公司從2014年開始投入技術改進資金，經技術改進后，其產品的成本不斷降低，具體數據如下表：
年度 | 投入技改資金 | 產品成本 |
2014 |
|
|
2015 | 3 | 12 |
2016 | 4 | 9 |
2017 |
| 8 |
（1）分析表中數據，請從一次函數和反比例函數中確定一個函數表示其變化規律，直接寫出y與x的函數關系式；
（2）按照這種變化規律，若2018年已投入資金6萬元．
①預計2018年每件產品成本比2017年降低多少萬元？
②若計劃在2018年把每件產品成本降低到5萬元，則還需要投入技改資金多少萬元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖,在△ABC中,點E在AC上,∠AEB=∠ABC.
(1)圖1中,作∠BAC的角平分線AD,分別交CB、BE于D、F兩點,求證:∠EFD=∠ADC；
(2)圖2中,作△ABC的外角∠BAG的角平分線AD,分別交CB、BE的延長線于D、F兩點,試探究(1)中結論是否仍成立?為什么?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，CD與⊙O相切于點C，與AB的延長線交于點D，DE⊥AD且與AC的延長線交于點E． 
（1）求證：DC=DE；
（2）若tan∠CAB= 
，AB=3，求BD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，客輪在海上以30km/h的速度由B向C航行，在B處測得燈塔A的方向角為北偏東80°，測得C處的方向角為南偏東25°，航行1小時后到達C處，在C處測得A的方向角為北偏東20°，則C到A的距離是（ ）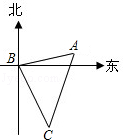
A.15 
km
B.15 
km
C.15（ + ）km
D.5（ +3 ）km
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（10分）如圖，已知線段AB上有兩點C，D，且AC＝BD，M，N分別是線段AC，AD的中點，若AB＝acm，AC＝BD＝bcm，且a，b滿足（a－10）2＋
＝0.
（1）求AB，AC的長度；
（2）求線段MN的長度.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，CD⊥AB，BE⊥AC，垂足分別為D，E，BE與CD相交于點O，且∠1=∠2，則下列結論正確的個數為( )
①B=∠C；②△ADO≌△AEO；③△BOD≌△COE；④圖中有四組三角形全等．
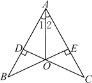
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
