
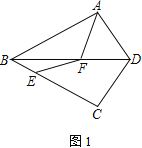
【題目】如圖,△ABD、△CBD關于直線BD對稱,點E是BC上一點,線段CE的垂直平分線交BD于點F,連接AF、EF.
(1) 求證:AF=EF;
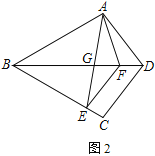
(2) 如圖2,連接AE交BD于點G.若EF∥CD,求證:![]() ;
;
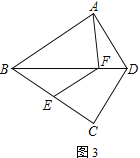
(3) 如圖3,若∠BAD=90°,且點E在BF的垂直平分線上,tan∠ABD=![]() ,DF=
,DF=![]() ,請直接寫出AF的長.
,請直接寫出AF的長.
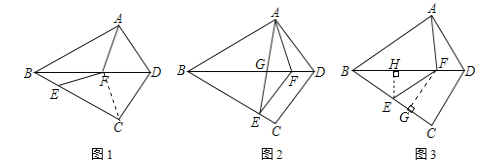
【答案】(1)CF=EF=AF(2)證明見解析(3)![]()
【解析】(1)如圖1,連接CF,根據軸對稱的性質和線段垂直平分線的性質證得結論;
(2)結合已知條件易證△ABD∽△EBF,則該相似三角形的對應邊成比例:![]() =
=![]() ,即
,即![]() =
=![]() .然后由角平分線定理推知
.然后由角平分線定理推知![]() =
=![]() ,所以根據等量代換證得
,所以根據等量代換證得![]() =
=![]() ;
;
(3)如圖3,過點E作EH⊥BD于H.結合銳角三角函數定義可以設EH=3a,BH=4a,則BE=EF=5a,BF=8a.過點F作FG⊥EC于G,在直角△GBF中,利用銳角三角函數定義求得線段FG、EG、BD的長度,則易得DF的長度,所以AF=EF=5a.
(1)如圖1,連接CF.
∵△ABD、△CBD關于直線BD對稱,線段CE的垂直平分線交BD于點F,∴CF=EF=AF,故AF=EF;
(2)由(1)可知:AF=EF.
∵△ABD、△CBD關于直線BD對稱,∴△ABD≌△CBD.
又∵EF∥CD,∴△CBD∽△EBF,∴△ABD∽△EBF,∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
又BD為∠ABC的平分線,∴![]() =
=![]() (角平分線定理),∴
(角平分線定理),∴![]() =
=![]() ;
;
(3)如圖3,過點E作EH
∵tan∠EBH=tan∠ABD=![]() ,設EH=3a,BH=4a,則HE=3a,BE=EF=5a,BF=8a.
,設EH=3a,BH=4a,則HE=3a,BE=EF=5a,BF=8a.
過點F作FG⊥EC于G,∴tan∠GBF=![]() ,∴FG=
,∴FG=![]() a,EG=CG=
a,EG=CG=![]() a,BC=BE+EG+GC=5a+
a,BC=BE+EG+GC=5a+![]() a+
a+![]() a=
a=![]() ,BD=
,BD=![]() a,∴DF=
a,∴DF=![]() a﹣8a=
a﹣8a=![]() a=
a=![]() ,a=
,a=![]() ,∴AF=5a=
,∴AF=5a=![]() .
.
故答案為:![]() .
.


 培優(yōu)口算題卡系列答案
培優(yōu)口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,∠MON=30°,點A1、A2、A3…在射線ON上,點B1、B2、B3…在射線OM上,△A1B1A2、△A2B2A3、△A3B3A4…均為等邊三角形,若OA1=1,則△A7B7A8的邊長為( )
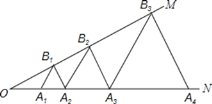
A. 64B. 32C. 16D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市以20元/件的價格購進一批商品,根據前期銷售情況,每天銷售量y(件)與該商品的銷售價x(元)之間的函數圖象如圖所示.
(1)求y與x之間的函數關系式.
(2)如果將該商品的銷售價定為30元/件,不考慮其它因素,求該超市每天銷售這種商品所能獲得的利潤.
(3)直接寫出能使該超市獲得最大利潤的商品銷售價
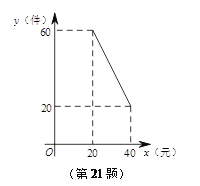
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E,F為BC上兩點,且BE=CF,連接AF,DE交于點O.求證:
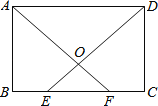
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知⊙O是△ABC的外接圓,AD是⊙O的直徑,且BD=BC,延長AD到E,BE是⊙O的切線,B是切點.
(1)求證:∠EBD=∠CAB;
(2)若BC=![]() ,AC=5,求sin∠CBA.
,AC=5,求sin∠CBA.
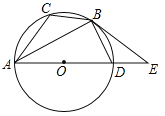
查看答案和解析>>
科目:初中數學 來源: 題型:
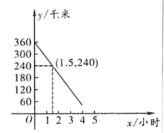
【題目】一輛旅游車從大理返回昆明,旅游車距昆明的路程y(千米)與行駛時間x(小時)之間的函數關系如圖所示,試回答下列問題:
(1)求此函數的表達式(不必求出自變量的取值范圍);
(2)若旅游車8:00從大理出發(fā),11:30在某加油站加油,問此時旅游車距昆明還有多少千米(途中停車時間不計)?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC中,點D,E分別在邊BC,AB上,且BD=AE,AD與CE交于點F,作CM⊥AD,垂足為M,下列結論不正確的是( )

A. AD=CE B. MF=![]() CF C. ∠BEC=∠CDA D. AM=CM
CF C. ∠BEC=∠CDA D. AM=CM
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中不正確的是( )
A. 等邊三角形是軸對稱圖形
B. 若兩個圖形的對應點連線都被同一條直線垂直平分,則這兩個圖形關于這條直線對稱
C. 若△ABC≌△![]() ,則這兩個三角形一定關于一條直線對稱
,則這兩個三角形一定關于一條直線對稱
D. 直線MN是線段AB的垂直平分線,若P點使PA=PB,則點P在MN上,若![]() ,則
,則![]() 不在MN上
不在MN上
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把 6個相同的小正方體擺成如圖的幾何體.
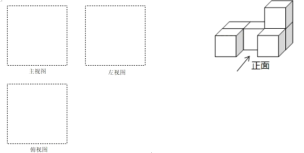
(1)畫出該幾何體的主視圖、左視圖、俯視圖;
(2)如果每個小正方體棱長為![]() ,則該幾何體的表面積是
,則該幾何體的表面積是 ![]() .
.
(3)如果在這個幾何體上再添加一些相同的小正方體,并并保持左視圖和俯視圖不變,那么最多可以再 添加 個小正方體.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com