
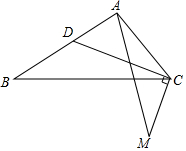
 如圖,△ABC中,∠ACB=α(0°<α<90°),CD平分∠ACB,過C點(diǎn)作CD的垂線交AB的垂直平分線于M,連接AM,求∠BAM(用含α的式子表示).
如圖,△ABC中,∠ACB=α(0°<α<90°),CD平分∠ACB,過C點(diǎn)作CD的垂線交AB的垂直平分線于M,連接AM,求∠BAM(用含α的式子表示). 分析 先連接BM,過M作MQ⊥AB于H,交CD的延長線于Q,連接AQ,BQ,根據(jù)MQ即為AB的垂直平分線,得出AQ=BQ,再過Q作QE⊥CA于E,作QF⊥BC于F,判定Rt△AEQ≌Rt△BFQ(HL),得出A,Q,B,C四點(diǎn)共圓,再根據(jù)∠QCM=90°,得出M在△BQC的外接圓上,即A,C,M,B,Q五點(diǎn)共圓,最后根據(jù)MB=MA,求得∠BAM=90°-$\frac{1}{2}$α.
解答 解:連接BM,過M作MQ⊥AB于H,交CD的延長線于Q,連接AQ,BQ,
由題可得,M在AB的垂直平分線上,
∴MQ即為AB的垂直平分線,
∴AQ=BQ,
過Q作QE⊥CA于E,作QF⊥BC于F,
∵在四邊形ACBQ中,CQ平分∠ACB,
∴QE=QF,
∴Rt△AEQ≌Rt△BFQ(HL),
∴∠QAE=∠QBF,
∵∠QAE+∠QAC=180°,
∴∠QBF+∠QAC=180°,
∴A,Q,B,C四點(diǎn)共圓,
∴QM垂直平分弦AB,圓心在QM上,
∵∠QCM=90°,
∴M在△BQC的外接圓上,
∴A,C,M,B,Q五點(diǎn)共圓,
∴∠AMB=∠ACB=α,
∵M(jìn)B=MA,
∴∠BAM=$\frac{180°-α}{2}$=90°-$\frac{1}{2}$α.
點(diǎn)評 本題主要考查了線段垂直平分線的性質(zhì),全等三角形的判定與性質(zhì),等腰三角形的性質(zhì)以及四點(diǎn)共圓的綜合應(yīng)用,解決問題的關(guān)鍵是作輔助線構(gòu)造全等三角形和等腰三角形.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
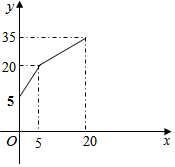 一個(gè)水槽有進(jìn)水管和出水管各一個(gè),進(jìn)水管每分鐘進(jìn)水m升,出水管每分鐘出水n升,水槽在開始5分鐘內(nèi)只進(jìn)水不出水,隨后15分鐘內(nèi)既進(jìn)水又出水,得到時(shí)間x(分)與水量y(升)之間的關(guān)系如圖所示:
一個(gè)水槽有進(jìn)水管和出水管各一個(gè),進(jìn)水管每分鐘進(jìn)水m升,出水管每分鐘出水n升,水槽在開始5分鐘內(nèi)只進(jìn)水不出水,隨后15分鐘內(nèi)既進(jìn)水又出水,得到時(shí)間x(分)與水量y(升)之間的關(guān)系如圖所示:查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
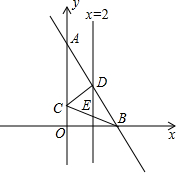 如圖,平面直角坐標(biāo)系中,直線AB:y=-2x+8交y軸于點(diǎn)A,交x軸于點(diǎn)B,以AB為底作等腰三角形△ABC的頂點(diǎn)C恰好落在y軸上,連接BC,直線x=2交AB于點(diǎn)D,交BC于點(diǎn)E,交x軸于點(diǎn)G,連接CD.
如圖,平面直角坐標(biāo)系中,直線AB:y=-2x+8交y軸于點(diǎn)A,交x軸于點(diǎn)B,以AB為底作等腰三角形△ABC的頂點(diǎn)C恰好落在y軸上,連接BC,直線x=2交AB于點(diǎn)D,交BC于點(diǎn)E,交x軸于點(diǎn)G,連接CD.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 在數(shù)軸上分別畫出點(diǎn)A、B、C、D,點(diǎn)A表示數(shù)$\frac{1}{3}$,點(diǎn)B表示數(shù)1$\frac{1}{2}$,點(diǎn)C表示數(shù)-2,點(diǎn)D表示數(shù)2$\frac{3}{4}$;并將點(diǎn)A、B、C、D所表示的數(shù)用“>”連接.
在數(shù)軸上分別畫出點(diǎn)A、B、C、D,點(diǎn)A表示數(shù)$\frac{1}{3}$,點(diǎn)B表示數(shù)1$\frac{1}{2}$,點(diǎn)C表示數(shù)-2,點(diǎn)D表示數(shù)2$\frac{3}{4}$;并將點(diǎn)A、B、C、D所表示的數(shù)用“>”連接.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com