Question

7．己知，點A、B分別在x軸、y軸上，M（m，m）是邊AB上的一點，CM⊥AB交X軸正半軸于點C．己知m滿足（m²+4m+3）-（m²-4）=15
（1）求M的坐標；
（2）如圖1，求OB+OC的值；
（3）如圖2，延長MC交y軸于點D，求S_△ACM-S_△OCD的值；
（4）如圖3，點P為AM上任意一點（P不與A、M重合），過A作AE⊥DP，點E為垂足，連EM，求∠DEM的度數．

Answer 1

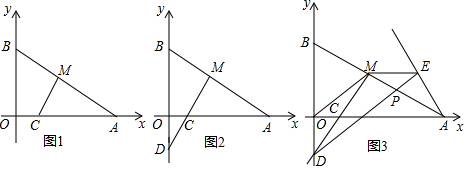
分析 （1）先解方程（m²+4m+3）-（m²-4）=15，求得m的值，即可得到M的坐標；
（2）如圖1，作輔助線，構建全等三角形，先證明四邊形OKMN為正方形得：OK=ON=2，再證明△MNB≌△MKC，則CK=BN，代入OB+OC中可得結論；
（3）如圖2，證明△AKM≌△DNM，則S_△AKM=S_△DNM，所以S_△ACM-S_△OCD拆成和與差的形式，并等量代換即可；
（4）如圖3，作輔助線，構建全等三角形，證明△MDF≌△MAE，得MF=ME，∠DMF=∠AME，再得△FME是等腰直角三角形，即可得出∠DEM=45°

解答 解：
（1）∵（m²+4m+3）-（m²-4）=15，
4m+3+4=15，
∴m=2，
∴M的坐標為（2，2）；
（2）如圖1，過M作KM⊥x軸，KN⊥y軸，垂足分別為K、N，

則∠MNO=∠MKO=90°，
∵∠BOA=90°，
∴四邊形OKMN是矩形，
∴∠NMK=90°，
∴∠NMC+∠CMK=90°，
∵M（2，2），
∴KM=MN=2，
∴矩形OKMN是正方形，
∴OK=ON=2，
∵CM⊥AB，
∴∠BMN+∠NMC=90°，
∴∠BMN=∠CMK，
∵∠MNB=∠CKM=90°，
∴△MNB≌△MKC（ASA），
∴CK=BN，
∴OB+OC=ON+BN+OC=ON+CK+OC=ON+OK=2+2=4；
（3）如圖2，∵∠AMC=∠KMN=90°，

∴∠AMK=∠NMD=90°-∠CMK，
∵∠MND=∠MKA=90°，KM=MN，
∴△AKM≌△DNM（ASA），
∴S_△AKM=S_△DNM，
∴S_△ACM-S_△OCD=S_△AKM+S_△CMK-S_△OCD
=S_△DNM+S_△CMK-S_△OCD
=S_{正方形OKMN}+S_△OCD-S_△OCD
=S_{正方形OKMN}
=2×2
=4；
（4）如圖3，由（3）得：△AKM≌△DNM，
∴AM=DM，
在DE上截取DF=AE，連接MF，

∵AE⊥EF，DM⊥AB，
∴∠DMP=∠AEP=90°，
∵∠MPD=∠EPA，
∴∠MDF=∠MAE，
∴△MDF≌△MAE（SAS），
∴MF=ME，∠DMF=∠AME，
∵∠DMP=90°，
∴∠DMF+∠FMP=∠AME+∠FMP=∠FME=90°，
∴△FME是等腰直角三角形，
∴∠DEM=45°．

點評 本題為三角形的綜合應用，涉及全等三角形、正方形、矩形的性質和判定等知識．解決問題的關鍵是證明三角形全等，利用全等三角形對應邊相等和對應角相等得出邊與角的關系；同時利用了全等三角形的面積相等，在求解三角形面積的差時，利用三角形面積相等關系進行加減，得出S_△ACM-S_△OCD的值與正方形的面積相等，從而得出結論．